After studying this Unit, you will be able to
Chemistry, by its very nature, is concerned with change. Substances with well defined properties are converted by chemical reactions into other substances with different properties. For any chemical reaction, chemists try to find out
(a) the feasibility of a chemical reaction which can be predicted by thermodynamics ( as you know that a reaction with ∆G < 0, at constant temperature and pressure is feasible);
(b) extent to which a reaction will proceed can be determined from chemical equilibrium;
(c) speed of a reaction i.e. time taken by a reaction to reach equilibrium.
Some reactions such as ionic reactions occur very fast, for example, precipitation of silver chloride occurs instantaneously by mixing of aqueous solutions of silver nitrate and sodium chloride. On the other hand, some reactions are very slow, for example, rusting of iron in the presence of air and moisture. Also there are reactions like inversion of cane sugar and hydrolysis of starch, which proceed with a moderate speed. Can you think of more examples from each category?
You must be knowing that speed of an automobile is expressed in terms of change in the position or distance covered by it in a certain period of time. Similarly, the speed of a reaction or the rate of a reaction can be defined as the change in concentration of a reactant or product in unit time. To be more specific, it can be expressed in terms of:
(i) the rate of decrease in concentration of any one of the reactants, or
(ii) the rate of increase in concentration of any one of the products.
Consider a hypothetical reaction, assuming that the volume of the system remains constant.
R → P
One mole of the reactant R produces one mole of the product P. If [R]1 and [P]1 are the concentrations of R and P respectively at time t1 and [R]2 and [P]2 are their concentrations at time t2 then,
∆t = t2 – t1
∆[R] = [R]2 – [R]1
∆ [P] = [P]2 – [P]1
The square brackets in the above expressions are used to express molar concentration.
Rate of disappearance of R  (4.1)
(4.1)
Rate of appearance of P  (4.2)
(4.2)
Since, ∆[R] is a negative quantity (as concentration of reactants is decreasing), it is multiplied with –1 to make the rate of the reaction a positive quantity.
Equations (4.1) and (4.2) given above represent the average rate of a reaction, rav.
Average rate depends upon the change in concentration of reactants or products and the time taken for that change to occur (Fig. 4.1).
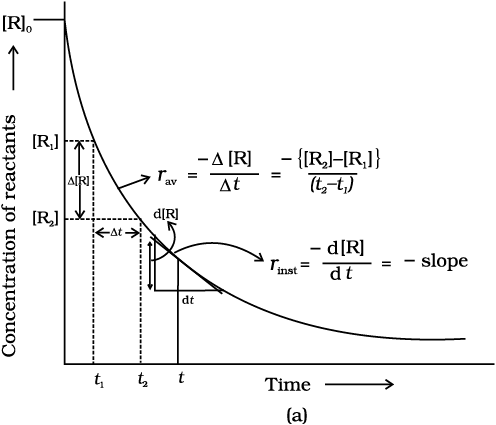
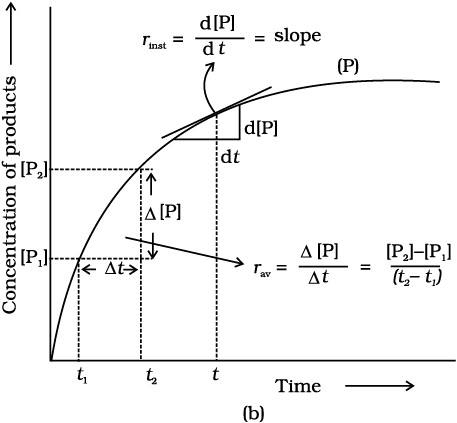
Fig. 4.1: Instantaneous and average rate of a reaction
Units of rate of a reaction
From equations (4.1) and (4.2), it is clear that units of rate are concentration time–1. For example, if concentration is in mol L–1 and time is in seconds then the units will be mol L-1s–1. However, in gaseous reactions, when the concentration of gases is expressed in terms of their partial pressures, then the units of the rate equation will be atm s–1.
Example 4.1
From the concentrations of C4H9Cl (butyl chloride) at different times given below, calculate the average rate of the reaction:
C4H9Cl + H2O → C4H9OH + HCl
during different intervals of time.
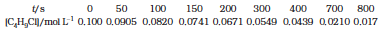
Solution
We can determine the difference in concentration over different intervals of time and thus determine the average rate by dividing ∆[R] by ∆t (Table 4.1).
Table 4.1: Average rates of hydrolysis of butyl chloride
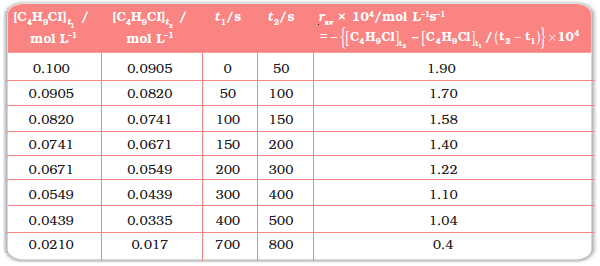
It can be seen (Table 4.1) that the average rate falls from 1.90× 0-4 mol L-1s-1 to 0.4 × 10-4 mol L-1s-1. However, average rate cannot be used to predict the rate of a reaction at a particular instant as it would be constant for the time interval for which it is calculated. So, to express the rate at a particular moment of time we determine the instantaneous rate. It is obtained when we consider the average rate at the smallest time interval say dt ( i.e. when ∆t approaches zero). Hence, mathematically for an infinitesimally small dt instantaneous rate is given by
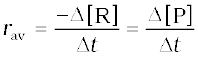 (4.3)
(4.3)
As ∆t → 0 or 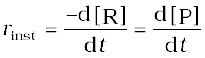
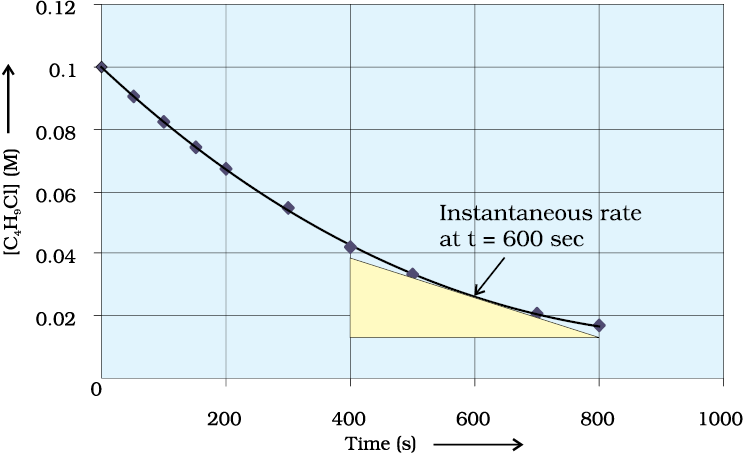
Fig 4.2 Instantaneous rate of hydrolysis of butyl chloride(C4H9Cl)
It can be determined graphically by drawing a tangent at time t on either of the curves for concentration of R and P vs time t and calculating its slope (Fig. 4.1). So in problem 4.1, rinst at 600s for example, can be calculated by plotting concentration of butyl chloride as a function of time. A tangent is drawn that touches the curve at t = 600 s (Fig. 4.2).
The slope of this tangent gives the instantaneous rate.
At t = 250 s rinst = 1.22 × 10–4 mol L–1s–1
t = 350 s rinst = 1.0 × 10–4 mol L–1s–1
t = 450 s rinst = 6.4 × 10–5 mol L–1s–1
Now consider a reaction
Hg(l) + Cl2 (g) → HgCl2(s)
Where stoichiometric coefficients of the reactants and products are same, then rate of the reaction is given as
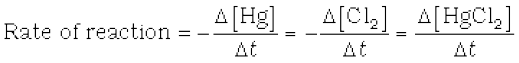
i.e., rate of disappearance of any of the reactants is same as the rate of appearance of the products. But in the following reaction, two moles of HI decompose to produce one mole each of H2 and I2,
2HI(g) → H2(g) + I2(g)
For expressing the rate of such a reaction where stoichiometric coefficients of reactants or products are not equal to one, rate of disappearance of any of the reactants or the rate of appearance of products is divided by their respective stoichiometric coefficients. Since rate of consumption of HI is twice the rate of formation of H2 or I2, to make them equal, the term ∆[HI] is divided by 2. The rate of this reaction is given by
Rate of reaction 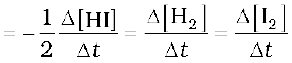
Similarly, for the reaction
5 Br- (aq) + BrO3– (aq) + 6 H+ (aq) → 3 Br2 (aq) + 3 H2O (l)
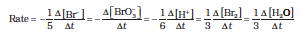
For a gaseous reaction at constant temperature, concentration is directly proportional to the partial pressure of a species and hence, rate can also be expressed as rate of change in partial pressure of the reactant or the product.
Example 4.2
The decomposition of N2O5 in CCl4 at 318K has been studied by monitoring the concentration of N2O5 in the solution. Initially the concentration of N2O5 is 2.33 mol L–1and after 184 minutes, it is reduced to 2.08 mol L–1. The reaction takes place according to the equation
2 N2O5 (g) → 4 NO2 (g) + O2 (g)
Calculate the average rate of this reaction in terms of hours, minutes and seconds. What is the rate of production of NO2 during this period?
Solution
Average Rate 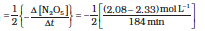
= 6.79 × 10–4 mol L–1/min = (6.79 × 10–4 mol L–1 min–1) × (60 min/1h)
= 4.07 × 10–2 mol L–1/h
= 6.79 × 10–4 mol L–1 × 1min/60s
= 1.13 × 10–5 mol L–1s–1
It may be remembered that
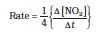
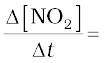 6.79 × 10–4 × 4 mol L–1 min–1 = 2.72 × 10–3 mol L–1min–1
6.79 × 10–4 × 4 mol L–1 min–1 = 2.72 × 10–3 mol L–1min–1
Intext Questions
4.1 For the reaction R → P, the concentration of a reactant changes from 0.03M to 0.02M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
4.2 In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L–1 to 0.4 mol L–1 in 10 minutes. Calculate the rate during this interval?
Rate of reaction depends upon the experimental conditions such as concentration of reactants (pressure in case of gases), temperature and catalyst.
The rate of a chemical reaction at a given temperature may depend on the concentration of one or more reactants and products. The representation of rate of reaction in terms of concentration of the reactants is known as rate law. It is also called as rate equation or rate expression.
The results in Table 4.1 clearly show that rate of a reaction decreases with the passage of time as the concentration of reactants decrease. Conversely, rates generally increase when reactant concentrations increase. So, rate of a reaction depends upon the concentration of reactants.
Consider a general reaction
aA + bB → cC + dD
where a, b, c and d are the stoichiometric coefficients of reactants and products.
The rate expression for this reaction is
Rate ∝ [A]x [B]y (4.4)
where exponents x and y may or may not be equal to the stoichiometric coefficients (a and b) of the reactants. Above equation can also be written as
Rate = k [A]x [B]y (4.4a)
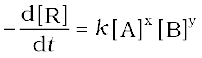 (4.4b)
(4.4b)
This form of equation (4.4 b) is known as differential rate equation, where k is a proportionality constant called rate constant. The equation like (4.4), which relates the rate of a reaction to concentration of reactants is called rate law or rate expression. Thus, rate law is the expression in which reaction rate is given in terms of molar concentration of reactants with each term raised to some power, which may or may not be same as the stoichiometric coefficient of the reacting species in a balanced chemical equation. For example:
2NO(g) + O2(g) → 2NO2 (g)
We can measure the rate of this reaction as a function of initial concentrations either by keeping the concentration of one of the reactants constant and changing the concentration of the other reactant or by changing the concentration of both the reactants. The following results are obtained (Table 4.2).
Table 4.2: Initial rate of formation of NO2
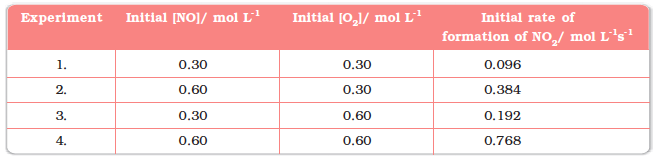
It is obvious, after looking at the results, that when the concentration of NO is doubled and that of O2 is kept constant then the initial rate increases by a factor of four from 0.096 to 0.384 mol L–1s–1. This indicates that the rate depends upon the square of the concentration of NO. When concentration of NO is kept constant and concentration of O2 is doubled the rate also gets doubled indicating that rate depends on concentration of O2 to the first power. Hence, the rate equation for this reaction will be
Rate = k[NO]2[O2]
The differential form of this rate expression is given as
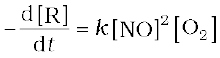
Now, we observe that for this reaction in the rate equation derived from the experimental data, the exponents of the concentration terms are the same as their stoichiometric coefficients in the balanced chemical equation.
Some other examples are given below:
In these reactions, the exponents of the concentration terms are not the same as their stoichiometric coefficients. Thus, we can say that:
Rate law for any reaction cannot be predicted by merely looking at the balanced chemical equation, i.e., theoretically but must be determined experimentally.
In the rate equation (4.4)
Rate = k [A]x [B]y
x and y indicate how sensitive the rate is to the change in concentration of A and B. Sum of these exponents, i.e., x + y in (4.4) gives the overall order of a reaction whereas x and y represent the order with respect to the reactants A and B respectively.
Hence, the sum of powers of the concentration of the reactants in the rate law expression is called the order of that chemical reaction.
Order of a reaction can be 0, 1, 2, 3 and even a fraction. A zero order reaction means that the rate of reaction is independent of the concentration of reactants.
Example 4.3
Calculate the overall order of a reaction which has the rate expression
(a) Rate = k [A]1/2 [B]3/2
(b) Rate = k [A]3/2 [B]–1
Solution
(a) Rate = k [A]x [B]y
order = x + y
So order = 1/2 + 3/2 = 2, i.e., second order
(b) order = 3/2 + (–1) = 1/2, i.e., half order.
A balanced chemical equation never gives us a true picture of how a reaction takes place since rarely a reaction gets completed in one step. The reactions taking place in one step are called elementary reactions. When a sequence of elementary reactions (called mechanism) gives us the products, the reactions are called complex reactions. These may be consecutive reactions (e.g., oxidation of ethane to CO2 and H2O passes through a series of intermediate steps in which alcohol, aldehyde and acid are formed), reverse reactions and side reactions (e.g., nitration of phenol yields o-nitrophenol and p-nitrophenol).
Units of rate constant
For a general reaction
aA + bB → cC + dD
Rate = k [A]x [B]y
Where x + y = n = order of the reaction
k = 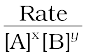
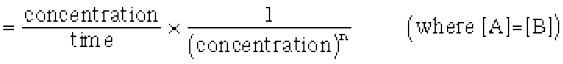
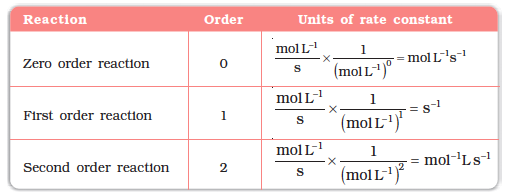
Taking SI units of concentration, mol L–1 and time, s, the units of k for different reaction order are listed in Table 4.3
Table 4.3: Units of rate constant
Example 4.4
Identify the reaction order from each of the following rate constants.
(i) k = 2.3 × 10–5 L mol–1 s–1
(ii) k = 3 × 10–4 s–1
Solution
(ii) The unit of a first order rate constant is s–1 therefore
k = 3 × 10–4 s–1 represents a first order reaction.
Another property of a reaction called molecularity helps in understanding its mechanism. The number of reacting species (atoms, ions or molecules) taking part in an elementary reaction, which must collide simultaneously in order to bring about a chemical reaction is called molecularity of a reaction. The reaction can be unimolecular when one reacting species is involved, for example, decomposition of ammonium nitrite.
NH4NO2 → N2 + 2H2O
Bimolecular reactions involve simultaneous collision between two species, for example, dissociation of hydrogen iodide.
2HI → H2 + I2
Trimolecular or termolecular reactions involve simultaneous collision between three reacting species, for example,
2NO + O2 → 2NO2
The probability that more than three molecules can collide and react simultaneously is very small. Hence, reactions with the molecularity three are very rare and slow to proceed.
It is, therefore, evident that complex reactions involving more than three molecules in the stoichiometric equation must take place in more than one step.
KClO3 + 6FeSO4 + 3H2SO4 → KCl + 3Fe2(SO4)3 + 3H2O
This reaction which apparently seems to be of tenth order is actually a second order reaction. This shows that this reaction takes place in several steps. Which step controls the rate of the overall reaction? The question can be answered if we go through the mechanism of reaction, for example, chances to win the relay race competition by a team depend upon the slowest person in the team. Similarly, the overall rate of the reaction is controlled by the slowest step in a reaction called the rate determining step. Consider the decomposition of hydrogen peroxide which is catalysed by iodide ion in an alkaline medium.
2H2O2 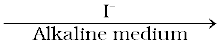 2H2O + O2
2H2O + O2
The rate equation for this reaction is found to be
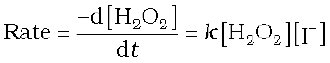
This reaction is first order with respect to both H2O2 and I–. Evidences suggest that this reaction takes place in two steps
(1) H2O2 + I– → H2O + IO–
(2) H2O2 + IO– → H2O + I– + O2
Both the steps are bimolecular elementary reactions. Species IO- is called as an intermediate since it is formed during the course of the reaction but not in the overall balanced equation. The first step, being slow, is the rate determining step. Thus, the rate of formation of intermediate will determine the rate of this reaction.
Thus, from the discussion, till now, we conclude the following:
(i) Order of a reaction is an experimental quantity. It can be zero and even a fraction but molecularity cannot be zero or a non integer.
(ii) Order is applicable to elementary as well as complex reactions whereas molecularity is applicable only for elementary reactions. For complex reaction molecularity has no meaning.
(iii) For complex reaction, order is given by the slowest step and molecularity of the slowest step is same as the order of the overall reaction.
4.3 For a reaction, A + B → Product; the rate law is given by, r = k [ A]1/2 [B]2. What is the order of the reaction?
4.4 The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y ?
The integrated rate equations are different for the reactions of different reaction orders. We shall determine these equations only for zero and first order chemical reactions.
Zero order reaction means that the rate of the reaction is proportional to zero power of the concentration of reactants. Consider the reaction,
R → P
Rate = 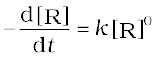
As any quantity raised to power zero is unity
Rate = 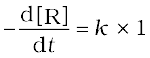
d[R] = – k dt
Integrating both sides
[R] = – k t + I (4.5)
where, I is the constant of integration.
At t = 0, the concentration of the reactant R = [R]0, where [R]0 is initial concentration of the reactant.
Substituting in equation (4.5)
[R]0 = –k × 0 + I
[R]0 = I
Substituting the value of I in the equation (4.5)
[R] = -kt + [R]0 (4.6)
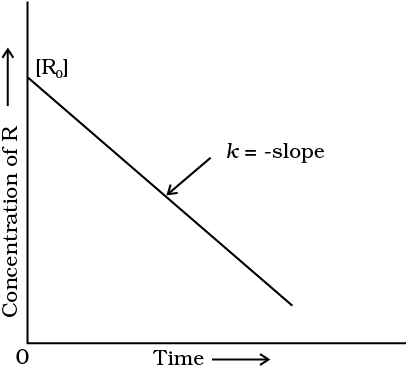
Further simplifying equation (4.6), we get the rate constant, k as
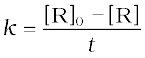 (4.7)
(4.7)
Zero order reactions are relatively uncommon but they occur under special conditions. Some enzyme catalysed reactions and reactions which occur on metal surfaces are a few examples of zero order reactions. The decomposition of gaseous ammonia on a hot platinum surface is a zero order reaction at high pressure.
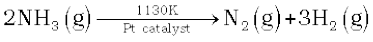
Rate = k [NH3]0 = k
In this reaction, platinum metal acts as a catalyst. At high pressure, the metal surface gets saturated with gas molecules. So, a further change in reaction conditions is unable to alter the amount of ammonia on the surface of the catalyst making rate of the reaction independent of its concentration. The thermal decomposition of HI on gold surface is another example of zero order reaction.
In this class of reactions, the rate of the reaction is proportional to the first power of the concentration of the reactant R. For example,
R → P
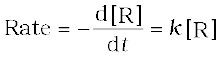
or 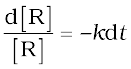
Integrating this equation, we get
ln [R] = –kt + I (4.8)
Again, I is the constant of integration and its value can be determined easily.
When t = 0, R = [R]0, where [R]0 is the initial concentration of the reactant.
Therefore, equation (4.8) can be written as
ln [R]0 = –k × 0 + I
ln [R]0 = I
Substituting the value of I in equation (4.8)
ln[R] = -kt + ln[R]0 (4.9)
Rearranging this equation
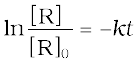
or 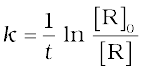 (4.10)
(4.10)
At time t1 from equation (4.8)
*ln[R]1 = – kt1 + *ln[R]0 (4.11)
At time t2
ln[R]2 = – kt2 + ln[R]0 (4.12)
where, [R]1 and [R]2 are the concentrations of the reactants at time t1 and t2 respectively.
Subtracting (4.12) from (4.11)
ln[R]1– ln[R]2 = – kt1 – (–kt2)
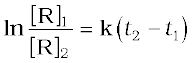
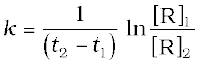 (4.13)
(4.13)
Equation (4.9) can also be written as
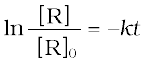
Taking antilog of both sides
[R] = [R]0 e-kt (4.14)
Comparing equation (4.9) with y = mx + c, if we plot ln [R] against t (Fig. 4.4) we get a straight line with slope = –k and intercept equal to ln [R]0
The first order rate equation (4.10) can also be written in the form
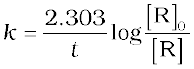 (4.15)
(4.15)
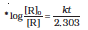
Hydrogenation of ethene is an example of first order reaction.
C2H4(g) + H2 (g) → C2H6(g)
Rate = k [C2H4]
* Refer to Appendix-IV for ln and log (logarithms).
All natural and artificial radioactive decay of unstable nuclei take place by first order kinetics.
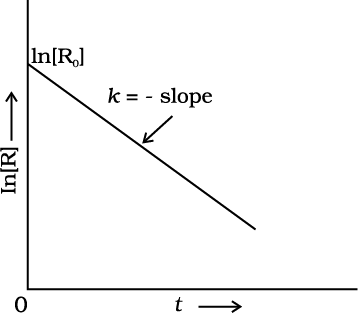
Fig. 4.4: A plot between ln[R] and t for a first order reaction
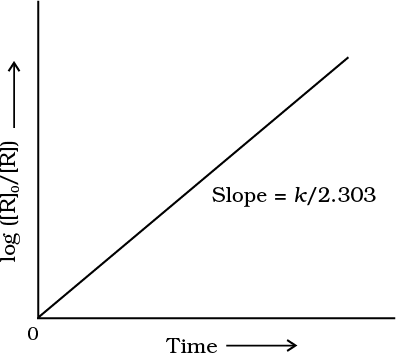
Fig. 4.5: Plot of log [R]0/[R] vs time for a first order reaction
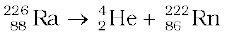
Example 4.5
The initial concentration of N2O5 in the following first order reaction N2O5(g) → 2 NO2(g) + 1/2O2 (g) was 1.24 × 10–2 mol L–1 at 318 K. The concentration of N2O5 after 60 minutes was 0.20 × 10–2 mol L–1. Calculate the rate constant of the reaction at 318 K.
Solution
For a first order reaction
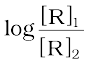 =
= 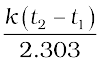
k = 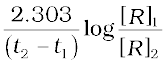
= 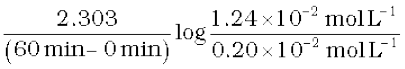
= 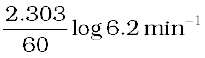
k = 0.0304 min-1
Let us consider a typical first order gas phase reaction
A(g) → B(g) + C(g)
Total pressure pt = pA + pB + pC (pressure units)
pA, pB and pC are the partial pressures of A, B and C, respectively.
If x atm be the decrease in pressure of A at time t and one mole each of B and C is being formed, the increase in pressure of B and C will also be x atm each.
where, pi is the initial pressure at time t = 0.
pt = (pi – x) + x + x = pi + x
x = (pt - pi)
where, pA = pi – x = pi – (pt – pi)
= 2pi – pt
k = 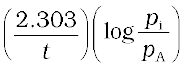 (4.16)
(4.16)
=
Example 4.6
The following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
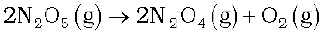

Calculate the rate constant.
Solution
Let the pressure of N2O5(g) decrease by 2x atm. As two moles of N2O5 decompose to give two moles of N2O4(g) and one mole of O2 (g), the pressure of N2O4 (g) increases by 2x atm and that of O2 (g) increases by x atm.
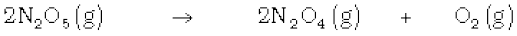
Start t = 0 0.5 atm 0 atm 0 atm
At time t (0.5 – 2x) atm 2x atm x atm
pt = 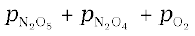
= (0.5 – 2x) + 2x + x = 0.5 + x
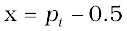
= 0.5 – 2x
= 0.5 – 2 (pt – 0.5) = 1.5 – 2pt
At t = 100 s; pt = 0.512 atm
= 1.5 – 2 × 0.512 = 0.476 atm
Using equation (4.16)
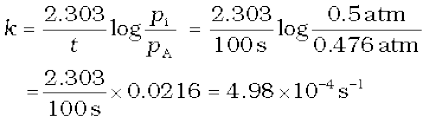
The half-life of a reaction is the time in which the concentration of a reactant is reduced to one half of its initial concentration. It is represented as t1/2.
For a zero order reaction, rate constant is given by equation 4.7.
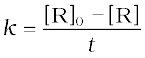
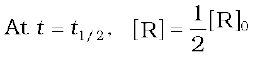
The rate constant at t1/2 becomes
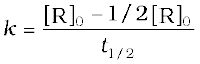
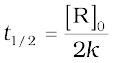
It is clear that t1/2 for a zero order reaction is directly proportional to the initial concentration of the reactants and inversely proportional to the rate constant.
For the first order reaction,
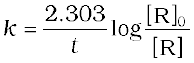 (4.15)
(4.15)
at t1/2 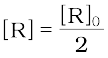 (4.16)
(4.16)
So, the above equation becomes
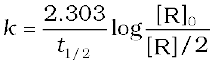
or 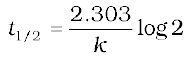
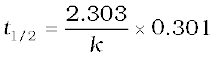
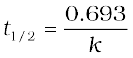 (4.17)
(4.17)
It can be seen that for a first order reaction, half-life period is constant, i.e., it is independent of initial concentration of the reacting species. The half-life of a first order equation is readily calculated from the rate constant and vice versa.
Example 4.7
A first order reaction is found to have a rate constant, k = 5.5 × 10-14 s-1. Find the half-life of the reaction.
Solution
Half-life for a first order reaction is
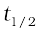 =
= 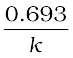
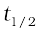 = =
= =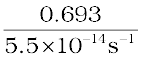 = 1.26 × 1013s
= 1.26 × 1013s
Example 4.8
Show that in a first order reaction, time required for completion of 99.9% is 10 times of half-life (t1/2) of the reaction.
When reaction is completed 99.9%, [R]n = [R]0 – 0.999[R]0
Solution
k = 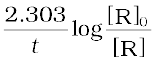
= 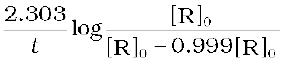 =
= 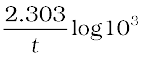
t = 6.909/k
For half-life of the reaction
t1/2 = 0.693/k
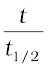 =
= 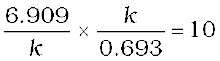
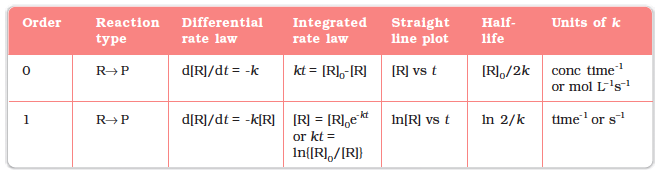
Table 4.4 summarises the mathematical features of integrated laws of zero and first order reactions.
Table 4.4: Integrated Rate Laws for the Reactions of Zero and First Order
The order of a reaction is sometimes altered by conditions. There are many reactions which obey first order rate law although they are higher order reactions. Consider the hydrolysis of ethyl acetate and water. In reality, it is a second order reactions and concentration of both ethyl acetate and water affect the rate of reaction. But water is taken in large excess for hydrolysis, therefore, concentration of water is not altered much during the reaction. Thus, the rate of reaction is affected by concentration of ethyl acetate with 10 mol of water, amounts of the reactants and products at the beginning (t=0) and completion (t) of the reaction are given as under.
CH3COOC2H5 + H2O 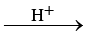 CH3COOH + C2H5OH
CH3COOH + C2H5OH
t = 0 0.01 mol 10 mol 0 mol 0 mol
t 0 mol 9.9 mol 0.01 mol 0.01 mol
The concentration of water does not get altered much during the course of the reaction. So, the reaction behaves as first order reaction. Such reactions are called pseudo first order reactions.
Inversion of cane sugar is another pseudo first order reaction.
C12H22O11 + H2O 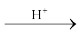 C6H12O6 + C6H12O6
C6H12O6 + C6H12O6
Cane sugar Glucose Fructose
Rate = k [C12H22O11]
Example 4.9
Hydrolysis of methyl acetate in aqueous solution has been studied by titrating the liberated acetic acid against sodium hydroxide. The concentration of the ester at different times is given below
t/min |
0 |
30 |
60 |
90 |
C/mol L-1 |
0.8500 |
0.8004 |
0.7538 |
0.7096 |
Show that it follows a pseudo first order reaction, as the concentration
of water remains nearly constant (55 mol L–1), during the course of the
reaction. What is the value of k′ in this equation?
Rate = k′ [CH3COOCH3][H2O]
Solution
For pseudo first order reaction, the reaction should be first order with
respect to ester when [H2O] is constant. The rate constant k for pseudo
first order reaction is
where
From the above data we note
t/min |
C/mol L-1 |
k’/min-1 |
0 |
0.8500 |
- |
30 |
0.8004 |
2.004 × 10-3 |
60 |
0.7538 |
2.002 × 10-3 |
90 |
0.7096 |
2.005 × 10-3 |
Intext Questions
4.5 A first order reaction has a rate constant 1.15 × 10-3 s-1. How long will 5 g of this reactant take to reduce to 3 g?
4.6 Time required to decompose SO2Cl2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
Most of the chemical reactions are accelerated by increase in temperature. For example, in decomposition of N2O5, the time taken for half of the original amount of material to decompose is 12 min at 50oC, 5 h at 25oC and 10 days at 0oC. You also know that in a mixture of potassium permanganate (KMnO4) and oxalic acid (H2C2O4), potassium permanganate gets decolourised faster at a higher temperature than that at a lower temperature.
It has been found that for a chemical reaction with rise in temperature by 10°, the rate constant is nearly doubled.
The temperature dependence of the rate of a chemical reaction can be accurately explained by Arrhenius equation (4.18). It was first proposed by Dutch chemist, J.H. van’t Hoff but Swedish chemist, Arrhenius provided its physical justification and interpretation.
k = A e -Ea /RT (4.18)
where A is the Arrhenius factor or the frequency factor. It is also called pre-exponential factor. It is a constant specific to a particular reaction. R is gas constant and Ea is activation energy measured in joules/mole (J mol –1).
It can be understood clearly using the following simple reaction
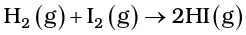
According to Arrhenius, this reaction can take place only when a molecule of hydrogen and a molecule of iodine collide to form an unstable intermediate (Fig. 4.6). It exists for a very short time and then breaks up to form two molecules of hydrogen iodide.

Fig. 4.6: Formation of HI through the intermediate
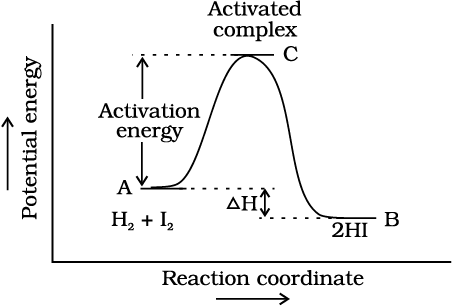
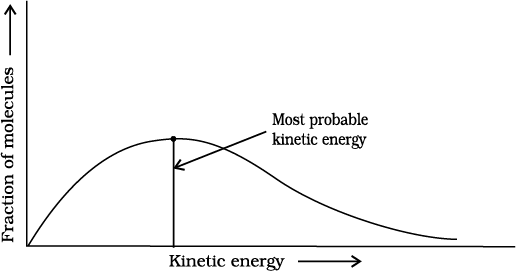
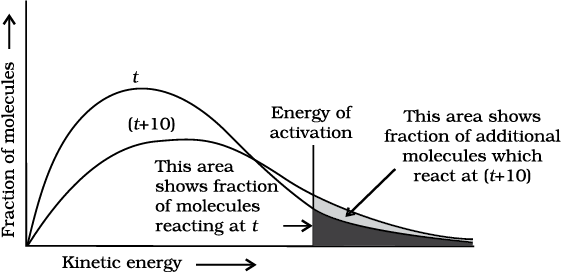
Fig. 4.9: Distribution curve showing temperature dependence of rate of a reaction
Increasing the temperature of the substance increases the fraction of molecules, which collide with energies greater than Ea. It is clear from the diagram that in the curve at (t+ 10), the area showing the fraction of molecules having energy equal to or greater than activation energy gets doubled leading to doubling the rate of a reaction.
In the Arrhenius equation (4.18) the factor e -Ea /RT corresponds to the fraction of molecules that have kinetic energy greater than Ea. Taking natural logarithm of both sides of equation (4.18)
ln k = –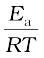 + ln A (4.19)
+ ln A (4.19)
The plot of ln k vs 1/T gives a straight line according to the equation (4.19) as shown in Fig. 4.10.
Thus, it has been found from Arrhenius equation (4.18) that increasing the temperature or decreasing the activation energy will result in an increase in the rate of the reaction and an exponential increase in the rate constant.
In Fig. 4.10, slope = – 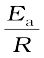 and intercept = ln A. So we can calculate Ea and A using these values.
and intercept = ln A. So we can calculate Ea and A using these values.
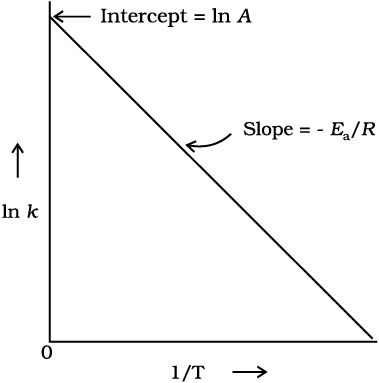
Fig. 4.10: A plot between ln k and 1/T
At temperature T1, equation (4.19) is
ln k1 = –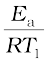 + ln A (4.20)
+ ln A (4.20)
At temperature T2, equation (4.19) is
ln k2 = –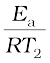 + ln A (4.21)
+ ln A (4.21)
(since A is constant for a given reaction)
k1 and k2 are the values of rate constants at temperatures T1 and T2 respectively.
Subtracting equation (4.20) from (4.21), we obtain
ln k2 – ln k1 = 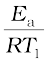 –
– 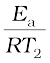
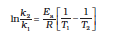
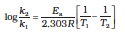 (4.22)
(4.22)
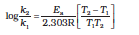
Example 4.10
The rate constants of a reaction at 500K and 700K are 0.02s–1 and 0.07s–1respectively. Calculate the values of Ea and A.
Solution
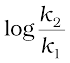 =
= 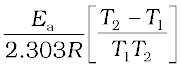
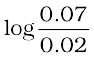 =
= 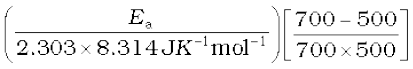
0.544 = Ea × 5.714 × 10-4/19.15
Ea = 0.544 × 19.15/5.714 × 10–4 = 18230.8 J
Since k = Ae-Ea/RT
0.02 = Ae-18230.8/8.314 × 500
A = 0.02/0.012 = 1.61
Example 4.11
The first order rate constant for the decomposition of ethyl iodide by the reaction
C2H5I(g) → C2H4 (g) + HI(g)
at 600K is 1.60 × 10–5 s–1. Its energy of activation is 209 kJ/mol. Calculate the rate constant of the reaction at 700K.
Solution
We know that
log k2 – log k1 = 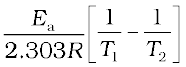
log k2 = 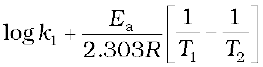
= 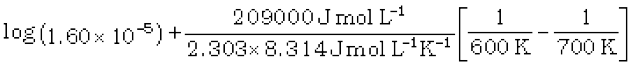
log k2 = – 4.796 + 2.599 = – 2.197
k2 = 6.36 × 10–3 s–1
A catalyst is a substance which increases the rate of a reaction without itself undergoing any permanent chemical change. For example, MnO2 catalyses the following reaction so as to increase its rate considerably.
2KClO3 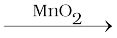 2 KCl + 3O2
2 KCl + 3O2
The word catalyst should not be used when the added substance reduces the rate of raction. The substance is then called inhibitor. The action of the catalyst can be explained by intermediate complex theory. According to this theory, a catalyst participates in a chemical reaction by forming temporary bonds with the reactants resulting in an intermediate complex. This has a transitory existence and decomposes to yield products and the catalyst.
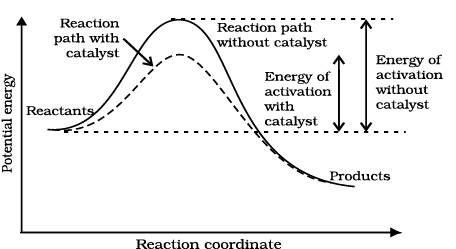
It is clear from Arrhenius equation (4.18) that lower the value of activation energy faster will be the rate of a reaction.
A small amount of the catalyst can catalyse a large amount of reactants. A catalyst does not alter Gibbs energy, ∆G of a reaction. It catalyses the spontaneous reactions but does not catalyse non-spontaneous reactions. It is also found that a catalyst does not change the equilibrium constant of a reaction rather, it helps in attaining the equilibrium faster, that is, it catalyses the forward as well as the backward reactions to the same extent so that the equilibrium state remains same but is reached earlier.
Though Arrhenius equation is applicable under a wide range of circumstances, collision theory, which was developed by Max Trautz and William Lewis in 1916 -18, provides a greater insight into the energetic and mechanistic aspects of reactions. It is based on kinetic theory of gases. According to this theory, the reactant molecules are assumed to be hard spheres and reaction is postulated to occur when molecules collide with each other. The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z). Another factor which affects the rate of chemical reactions is activation energy (as we have already studied). For a bimolecular elementary reaction
A + B → Products
rate of reaction can be expressed as
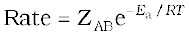 (4.23)
(4.23)
where ZAB represents the collision frequency of reactants, A and B and e-Ea /RTrepresents the fraction of molecules with energies equal to or greater than Ea. Comparing (4.23) with Arrhenius equation, we can say that A is related to collision frequency.
Equation (4.23) predicts the value of rate constants fairly accurately for the reactions that involve atomic species or simple molecules but for complex molecules significant deviations are observed. The reason could be that all collisions do not lead to the formation of products. The collisions in which molecules collide with sufficient kinetic energy (called threshold energy*) and proper orientation, so as to facilitate breaking of bonds between reacting species and formation of new bonds to form products are called as effective collisions.
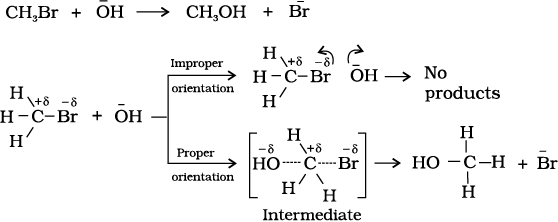
Fig. 4.12: Diagram showing molecules having proper and improper orientation
To account for effective collisions, another factor P, called the probability or steric factor is introduced. It takes into account the fact that in a collision, molecules must be properly oriented i.e.,
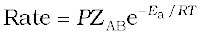
Thus, in collision theory activation energy and proper orientation of the molecules together determine the criteria for an effective collision and hence the rate of a chemical reaction.
Collision theory also has certain drawbacks as it considers atoms/molecules to be hard spheres and ignores their structural aspect. You will study details about this theory and more on other theories in your higher classes.
Intext Questions
4.7 What will be the effect of temperature on rate constant ?
4.8 The rate of the chemical reaction doubles for an increase of 10K in absolute temperature from 298K. Calculate Ea.
4.9 The activation energy for the reaction
2 HI(g) → H2 + I2 (g)
is 209.5 kJ mol–1 at 581K.Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Chemical kinetics is the study of chemical reactions with respect to reaction rates, effect of various variables, rearrangement of atoms and formation of intermediates. The rate of a reaction is concerned with decrease in concentration of reactants or increase in the concentration of products per unit time. It can be expressed as instantaneous rate at a particular instant of time and average rate over a large interval of time. A number of factors such as temperature, concentration of reactants, catalyst, affect the rate of a reaction. Mathematical representation of rate of a reaction is given by rate law. It has to be determined experimentally and cannot be predicted. Order of a reaction with respect to a reactant is the power of its concentration which appears in the rate law equation. The order of a reaction is the sum of all such powers of concentration of terms for different reactants. Rate constant is the proportionality factor in the rate law. Rate constant and order of a reaction can be determined from rate law or its integrated rate equation. Molecularity is defined only for an elementary reaction. Its values are limited from 1 to 3 whereas order can be 0, 1, 2, 3 or even a fraction. Molecularity and order of an elementary reaction are same.
 .
.
Intext Questions
4.1: For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
NEETprep Answer4.2: In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L to 0.4 mol Lin 10 minutes. Calculate the rate during this interval?
NEETprep Answer4.3: For a reaction, A + B → Product; the rate law is given by, . What is the order of the reaction?
NEETprep Answer
4:4The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y?
4.5: A first order reaction has a rate constant 1.15 10−3 s−1 How long will 5 g of this reactant take to reduce to 3 g?
NEETprep Answer4.6: Time required to decompose SO2Cl2 to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
NEETprep Answer4.7: What will be the effect of temperature on rate constant?
NEETprep Answer4:8The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate Ea.
NEETprep Answer
Question 4.9:The activation energy for the reaction
2HI(g) → H2 + I2(g)
is 209.5 kJ mol−1 at 581K. Calculate the fraction of molecules of reactants having energy
equal to or greater than activation energy?
4.1 From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3NO(g) → N2O (g) Rate = k[NO]2
(ii) H2O2 (aq) + 3I– (aq) + 2H+ → 2H2O (l) + Rate = k[H2O2][I-]
(iii) CH3CHO (g) → CH4 (g) + CO(g) Rate = k[CH3CHO]3/2
(iv) C2H5Cl (g) → C2H4 (g) + HCl (g) Rate = k[C2H5Cl]
NEETprep Answer4.2 For the reaction:
2A + B → A2B
the rate = k[A][B]2 with k = 2.0 × 10–6 mol–2 L2 s–1. Calculate the initial rate of the reaction when [A] = 0.1 mol L–1, [B] = 0.2 mol L–1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L–1.
NEETprep Answer4.3 The decomposition of NH3 on platinum surface is zero order reaction. What are the rates of production of N2 and H2 if k = 2.5 × 10–4 mol–1 L s–1?
NEETprep Answer
4.4 The decomposition of dimethyl ether leads to the formation of CH4, H2 and CO and the reaction rate is given by
Rate = k [CH3OCH3]3/2
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
Rate=K
If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
NEETprep Answer4.5 Mention the factors that affect the rate of a chemical reaction.
NEETprep Answer4.6 A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is
(i) doubled (ii) reduced to half ?
NEETprep Answer4.7 What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on rate constant be represented quantitatively?
NEETprep Answer4.8 In a pseudo first order reaction in water, the following results were obtained:

(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
NEETprep Answer4.9 A reaction is first order in A and second order in B.
NEETprep Answer(i) Write the differential rate equation.
(ii) How is the rate affected on increasing the concentration of B three times?
(iii) How is the rate affected when the concentrations of both A and B are doubled?
4.10 In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:

What is the order of the reaction with respect to A and B?
NEETprep Answer
4.11 The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D
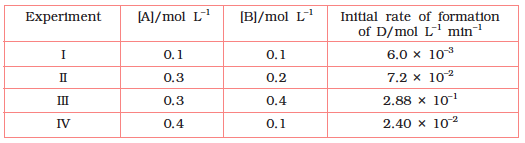
Determine the rate law and the rate constant for the reaction.
NEETprep Answer
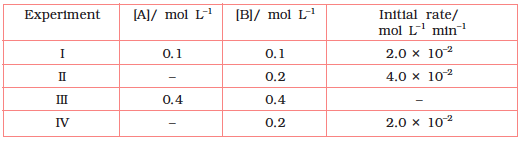
4.12 The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
4.13 Calculate the half-life of a first order reaction from their rate constants given below:
(i) 200 s–1 (ii) 2 min–1 (iii) 4 years–1
NEETprep Answer4.14 The half-life for radioactive decay of 14C is 5730 years. An archaeological artifact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.
NEETprep Answer
4.15 The experimental data for decomposition of N2O5
[2N2O5 → 4NO2 + O2]
in gas phase at 318K are given below:

(i) Plot [N2O5] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log[N2O5] and t.
(iv) What is the rate law ?
(v) Calculate the rate constant.
(vi) Calculate the half-life period from k and compare it with (ii).
NEETprep Answer4.16 The rate constant for a first order reaction is 60 s–1. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
It is known that,
NEETprep Answer4.17 During nuclear explosion, one of the products is 90Sr with half-life of 28.1 years. If 1µg of 90Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
NEETprep Answer4.18 For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
NEETprep Answer4.19 A first order reaction takes 40 min for 30% decomposition. Calculate t1/2.
NEETprep Answer4.20 For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
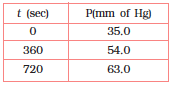
Calculate the rate constant.
NEETprep Answer4.21 The following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume.
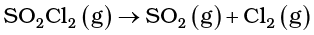
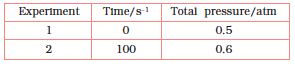
Calculate the rate of the reaction when total pressure is 0.65 atm.
NEETprep Answer4.22 The rate constant for the decomposition of N2O5 at various temperatures is given below:

Draw a graph between ln k and 1/T and calculate the values of A and Ea. Predict the rate constant at 30° and 50°C.
NEETprep Answer4.23 The rate constant for the decomposition of hydrocarbons is 2.418 × 10–5s–1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.
NEETprep Answer4.24 Consider a certain reaction A → Products with k = 2.0 × 10–2s–1. Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L–1.
NEETprep Answer4.25 Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t1/2 = 3.00 hours. What fraction of sample of sucrose remains after 8 hours ?
NEETprep Answer4.26 The decomposition of hydrocarbon follows the equation
k = (4.5 × 1011s–1) e-28000K/T
Calculate Ea. For the reaction R
NEETprep Answer4.27 The rate constant for the first order decomposition of H2O2 is given by the following equation:
log k = 14.34 – 1.25 × 104K/T
Calculate Ea for this reaction and at what temperature will its half-period be 256 minutes?
NEETprep Answer4.28 The decomposition of A into product has value of k as 4.5 × 103 s–1 at 10°C and energy of activation 60 kJ mol–1. At what temperature would k be 1.5 × 104s–1?
4.29 The time required for 10% completion of a first order reaction at 298K is equal to that required for its 25% completion at 308K. If the value of A is 4 × 1010s–1. Calculate k at 318K and Ea.
NEETprep Answer4.30 The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
NEETprep AnswerExemplar Questions
Q.1 The role of a catalyst is to change.
(a) Gibbs energy of the reaction
(b) enthalpy of reaction
(c) the activation energy of the reaction
(d) equilibrium constant
NEETprep Answer
Q.2 In the presence of a catalyst, the heat evolved or absorbed during the reaction
(a) increases
(b) decreases
(c) remains unchanged
(d) may increase or decrease
NEETprep Answer
Q.3 Activation energy of a chemical reaction can be determined by ...
(a) determining the rate constant at standard temperature
(b) determining the rate constant at two temperatures
(c) determining probability of collision
(d) using the catalyst
NEETprep Answer
Q.4 Consider figure and mark the correct option.
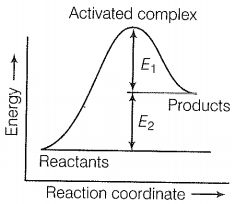
(a) Activation energy of forwarding reaction is and the product is less stable than reactant
(b) Activation energy of forwarding reaction is and the product is more stable than the reactant
(c) Activation energy of both forward and backward reaction is and reactant IS more stable than the product
(d) Activation energy of the backward reaction is E1 and the product is more stable than reaction
NEETprep Answer
Q.5 Consider a first-order gas-phase decomposition reaction given below
The initial pressure of the system before decomposition of A was pi. After the lapse of time, 't total pressure of the system increased by X units and became pPt. The rate constant k for the reaction 1s given as
NEETprep Answer
Q.6 According to Arrhenius equation rale constant k is equal to . Which of the following options represents the graph of ln k vs1/T?
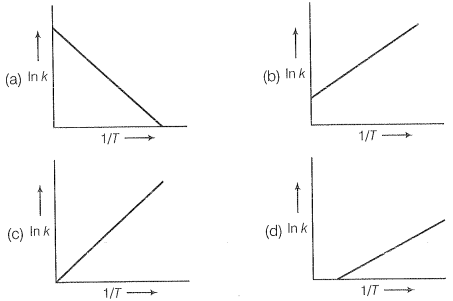
Q.7 Consider the Arrhenius equation given below and mark the correct option.
(a) Rate constant increases exponentially with increasing activation energy and decreasing temperature
(b) Rate constant decreases exponentially with increasing activation energy and decreasing temperature
(c) Rate constant increases exponentially with decreasing activation energy and decreasing temperature
(d) Rate constant increases exponentially with decreasing activation energy and increasing temperature
NEETprep Answer
Q.8 A graph of volume of hydrogen released vs time for the reaction between zinc and dit. HCl is given in the figure. On the basis of this mark the correct option.
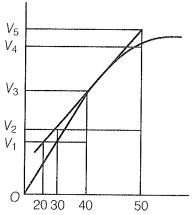
Q.9Which of the following statements is not correct about the order of a reaction?
(a) The order of a reaction can be a fractional number
(b) Order of a reaction is experimentally determined quantity
(c) The order of a reaction is always equal to the sum of the stoichiometric coefficients of reactants in the balanced chemical equation for a reaction
(d) The order of a reaction is the sum of the powers of the molar concentration of the reactants in the rate law expression
NEETprep Answer
Q. 10 Consider the graph given in the figure. Which of the following options does not show an instantaneous rate of reaction in the 40s?
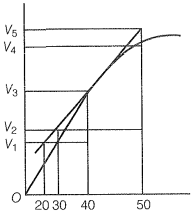
Q.11 Which of the following statements is correct?
(a) The rate of a reaction decreases with the passage of time as they concentrate on of reactants decreases
(b) The rate of a reaction is the same at any time during the reaction
(c) The rate of a reaction is independent of temperature change
(d) The rate of a reaction decreases with an increase in the concentration of the reactant (s)
NEETprep Answer
Q.12 Which of the following expressions is correct for the rate of reaction given below?
NEETprep Answer
Q.13 Which of the following graphs represents an exothermic reaction?
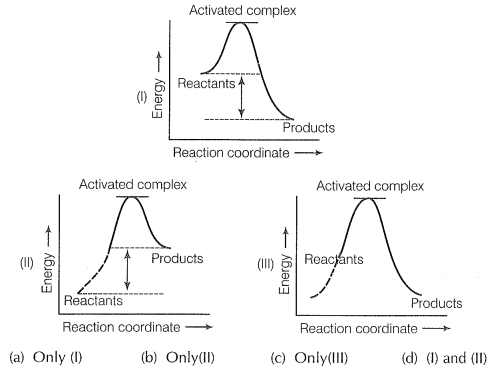
Q. 14 Rate law for the reaction A+ 2B -> C is found to be
Rate = k[A][B]
The concentration of reactant 'B is doubled, keeping the concentration of A constant, the value of the rate constant will be...
(a) the same
(b) doubled
(c) quadrupled
(d) halved
NEETprep Answer
Q.15 Which of the following statements is incorrect about the collision theory of chemical reaction?
(a) It considers reacting molecules or atoms to be hard spheres and ignores their structural features
(b) Number of effective collisions determines the rate of reaction
(c) Collision of atoms or molecules possessing sufficient threshold energy results in the product formation
(d) Molecules should collide orientation for the collision to be effective with sufficient threshold energy and proper
NEETprep Answer
Q.16 A first-order reaction is 50% completed in 1. 26 x s. How much time would it take for 100% completion?
NEETprep Answer
Q.17 Compounds A and 'B' react according to the following chemical equation.
(Ag) + 2B(g) 2C(g)
The concentration of either or or 'B was changed keeping the concentrations of one of the reactants constant and rates were measured as a function of initial concentration. The following results were obtained. Choose the correct option for the rate equations for this reaction.
| Experiment |
Initial concentration of [A]/mol L-1 |
Initial concentration of [B]/moI L-1 |
Initial concentration of [C]/mol L-1 s-1 |
|
1. 2. 3. |
0.30 0.30 0.60 |
0.30 0.60 0.30 |
0.20 0.40 0.20 |
NEETprep Answer
Q.18 Which of the following statement is not correct for the catalyst?
(a) It catalyzes the forward and backward reactions to the same extent
(b) It alters AG of the reaction
(c) It is a substance that does not change the equilibrium constant of a reaction
(d) It provides an alternate mechanism by reducing activation energy between reactants and products
NEETprep Answer
Q.19 The value of rate constant of a pseudo-first-order reaction..
(a) depends on the concentration of reactants present in a small amount
(b) depends on the concentration of reactants present in excess
(c) is independent of the concentration of reactants
(d) depends only on temperature
NEETprep Answer
Q, 20 Consider the reaction A B. The concentration of both the reactants and the products varies exponentially with time. Which of the following figures correctly describes the change in concentration of reactants and products with time?
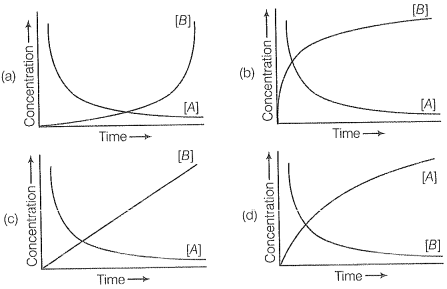
Exemplar Questions
Q.21 Rate law cannot be determined from a balanced chemical equation if.
(a) the reverse reaction is involved
(b) it is an elementary reaction
(c) it is a sequence of elementary reactions
(d) any of the reactants is in excess
Q.22 Which of the following statements are applicable to a balanced chemical equation of an elementary reaction?
(a) Order is the same as molecularity
(b) Order is less than the molecularity
(c) Order is greater than the molecularity
(d) Molecularity can never be zero
Q.23 In any unimolecular reaction.
(a) only one reacting species is involved in the rate-determining step
(b) the order and the molecularity of the slowest step are equal to one
(c) the molecularity of the reaction is one and order is zero
(d) both molecularity and order of the reaction are one
Q.24 For a complex reaction.
(a) order of the overall reaction is the same as the molecularity of the slowest step
(b) order of the overall reaction is less than the molecularity of the slowest step
(c) order of the overall reaction is greater than the molecularity of the slowest step
(d) the molecularity of the slowest step is never zero or non-integer
Q.25 At high pressure the following reaction is zero order.
Which of the following options are correct for this reaction?
(a) Rate of reaction Rate constant
(b) Rate of the reaction depends on the concentration of ammonia
(c)Rate of decomposition of ammonia will remain constant until ammonia disappears completely
(d) Further increase in pressure will change the rate of reaction
26 During decomposition of an activated complex
(a) energy is always released
(b) energy is always absorbed
(c) energy does not change
(d) reactants may be formed
0.27 According to Maxwell, Boltzmann distribution of energy.
(a) the fraction of molecules with the most probable kinetic energy decreases at higher temperatures
(b) the fraction of molecules with the most probable kinetic energy increases at higher temperatures
(c) most probable kinetic energy increases at higher temperatures
(d) most probable kinetic energy decreases at higher temperatures
Q.28 In the graph showing Maxwell, Boltzmann distribution of energy......
(a) the area under the curve must not change with an increase in temperature
(b) the area under the curve increases with increase in temperature
(c) area under the curve decreases with increase in temperature
(d) with an increase in temperature curve broadens and shifts to the right-hand side
Q. 29 Which of the following statements are in accordance with the Arrhenius equation?
(a) Rate of a reaction increases with an increase in temperature
(b) Rate of a reaction increases with a decrease in activation energy
(c) Rate constant decreases exponentially with an increase in temperature
(d) Rate of reaction decreases with a decrease in activation energy
Q.30 Mark the incorrect statements.
(a) Catalyst provides an alternative pathway to the reaction mechanism
(b) Catalyst raises the activation energy
(c) Catalyst lowers the activation energy
(d) Catalyst alters enthalpy change of the reaction
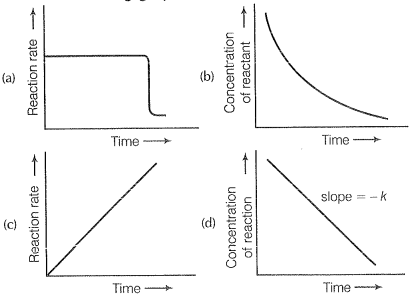
Q.31 Which of the following graphs is correct for a zero-order reaction:
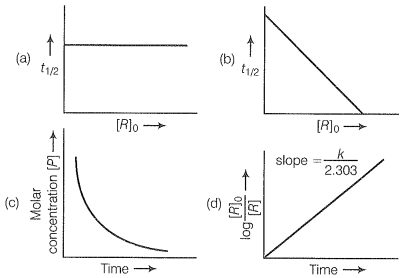
Q.32 Which of the following graphs is correct for a first-order reaction?
Q.33 State a condition under which a bimolecular reaction is a kinetically first-order reaction.
NEETprep Answer
Q.34 Write the rate equation for the reaction 24+ B C if the order of the reaction is zero.
NEETprep Answer
Q.35 How can you determine the rate law of the following reaction?
NEETprep Answer
Q.36 For which type of reactions, order, and molecularity have the same value?
NEETprep Answer
Q37 In a reaction if the concentration of reactant A is tripled, the rate of reaction becomes twenty-seven times. What is the order of the reaction?
NEETprep Answer
38 Derive an expression to calculate the time required for completion of the zero-order reaction.
NEETprep Answer
Q.39 For a reaction A +B Products, the rate law is-Rate = k[A][B]3/2. Can the reaction be an elementary reaction: Explain.
NEETprep Answer
Q.40 For a certain reaction large fraction of molecules have energy more than the threshold energy, yet the rate of reaction is very slow. Why?
NEETprep AnswerExemplar Questions
Q.41 For a zero-order reaction will the molecularity be equal to zero? Explain.
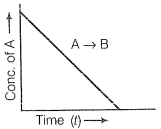
Q.42 For a general reaction A B, plot of concentration of A vs time is given in the figure. Answer the following questions on the basis of this graph.
(i) What is the order of the reaction?
(ii) What is the slope of the curve?
(iii) What are the units of the rate constant?
Q.43 The reaction between (g) and (g) is highly feasible yet allowing the gases to stand at room temperature in the same vessel does not lead to the formation of water. Explain.
Q.44 Why does the rate of a reaction increase with rising temperatures?
Q.45 0xygen is available in plenty in the air yet fuels do not burn by themselves at room temperature. Explain.
Q.46 What is the probability of reaction with molecularity higher than three very rare?
Q.47 Why does the rate of any reaction generally decreases during the course or the reaction?
Q.48 Thermodynamic feasibility of the reaction alone cannot decide the rate of the reaction. Explain with the help of one example.
Q.49 Why in the redox titration of KMnO4, vs Oxalic acid, we heat oxalic acid solution before starting the titration?
Q.50 Why can't the molecularity of any reaction be equal to zero?
Q.51 Why molecularity is applicable only for elementary reactions and order is applicable for elementary as well as complex reactions
NEETprep Answer
Q.52 Why can we not determine the order of a reaction by taking into consideration the balanced chemical equation?
NEETprep Answer
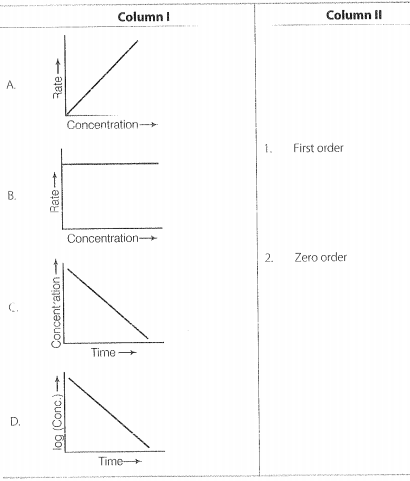
Q.53 Match the graph given in Column I with the order of reaction given in Column II. More than one item in Column I may link to the same item of Column II.
Q.54 Match the statements given in Column I and Column II.
| Column I | Column II |
A. Catalyst alters the rate of reaction |
1. Cannot be fraction ur zero 2. Proper orientation is not there 3. By 'owering the activation energy 4. Is same as the first 5. Total probability is one 6. Refers to the fraction of molecules with energy equal tö or greater than activation energy |
NEETprep Answer
Q.55 Match the items of Column I and Column II.
| Column I | Column II |
|
A. Diamond B. Instantaneous rate C. Average rate ¯ |
1. Short interval of time 2. Ordinarily rate of conversion is imperceptible 3. Long duration of time |
NEETprep Answer
Q.56 Match the items of Column I and Column II.
| Column I | Column II |
|
A. Mathematical expression for rate of reaction B. Rate of reaction for zero order reaction is equal to C. units ot rate constant for zero order reaction is same as that of D. Order of a complex reaction is determined by |
1. Rate constant 2. Rate law 3. Order of slowest step 4. Rate of reaction |
NEETprep Answer
Assertion and Reason
In the following questions, a statement of Assertion (A) followed by a statement: of Reason (R) is given. Choose the correct answer out of the following choices.
(a) Both assertion and reason are correct and the reason is the correct explanation of assertion.
(b) Both assertion and reason are correct, but reason does not explain the assertion
(c)Assertion is correct, but the reason is incorrect.
(d) Both assertion and reason are incorrect.
(e) The assertion is incorrect, but the reason is correct.
Q.57 Assertion (A) Order of the reaction can be zero or fractional.
Reason (R) We cannot determine order from the balanced chemical equation.
NEETprep Answer
Q.58 Assertion (A) Order and molecularity are the same.
Reason (R) Order is determined experimentally and molecularity is the Sum of the stoichiometric coefficient of the rate-determining elementary step.
NEETprep Answer
Q.59 Assertion (A) The enthalpy of reaction remains constant in the presence of a catalyst.
Reason (R) A catalyst participating in the reaction forms a different activated complex and lowers down the activation energy but the difference in energy of reactant and product remains the same.
NEETprep Answer
Q.60 Assertion (A) All collisions of reactant molecules lead to product formation.
Reason (R) Only those collisions in which molecules have correct orientation and sufficient kinetic energy lead to the compound formation.
NEETprep Answer
Assertion and Reason
In the following questions, a statement of Assertion (A) followed by a statement: of Reason (R) is given. Choose the correct answer out of the following choices.
(a) Both assertion and reason are correct and the reason is the correct explanation of assertion.
(b) Both assertion and reason are correct, but reason does not explain the assertion
(c)Assertion is correct, but the reason is incorrect.
(d) Both assertion and reason are incorrect.
(e) The assertion is incorrect, but the reason is correct.
Q.61 Assertion (A) Rate constant determined from the Arrhenius equation is fairly accurate for simple as well as complex molecules.
Reason (R) Reactant molecules undergo chemical change irrespective of their orientation during a collision.
NEETprep Answer
Q.62 All energetically effective collisions do not result in a chemical change. Explain with the help of an example.
NEETprep Answer
Q.63 What happens to most probable kinetic energy and the energy of activation with an increase in temperature?
NEETprep Answer
Q.64 Describe how does the enthalpy of reaction remains unchanged when a catalyst is used in the reaction?
NEETprep Answer
Q.65 Explain the difference between the instantaneous rate of a reaction and the average rate of a reaction.
NEETprep Answer
Q.66 With the help of an example explain what is meant by the pseudo-first-order reaction.
NEETprep Answer