Knowledge of mathematical tools and kinematics is essential before starting this chapter.
6.1 Introduction
6.2 Notions of work and kinetic energy : The work-energy theorem
6.3 Work
6.4 Kinetic energy
6.5 Work done by a variable force
6.6 The work-energy theorem for a variable force
6.7 The concept of potential energy
6.8 The conservation of mechanical energy
6.9 The potential energy of a spring
6.10 Various forms of energy : the law of conservation of energy
6.11 Power
6.12 Collisions
Summary
Points to ponder
Exercises
Additional exercises
Appendix 6.1
The terms ‘work’, ‘energy’ and ‘power’ are frequently used in everyday language. A farmer ploughing the field, a construction worker carrying bricks, a student studying for a competitive examination, an artist painting a beautiful landscape, all are said to be working. In physics, however, the word ‘Work’ covers a definite and precise meaning. Somebody who has the capacity to work for 14-16 hours a day is said to have a large stamina or energy. We admire a long distance runner for her stamina or energy. Energy is thus our capacity to do work. In Physics too, the term ‘energy’ is related to work in this sense, but as said above the term ‘work’ itself is defined much more precisely. The word ‘power’ is used in everyday life with different shades of meaning. In karate or boxing we talk of ‘powerful’ punches. These are delivered at a great speed. This shade of meaning is close to the meaning of the word ‘power’ used in physics. We shall find that there is at best a loose correlation between the physical definitions and the physiological pictures these terms generate in our minds. The aim of this chapter is to develop an understanding of these three physical quantities. Before we proceed to this task, we need to develop a mathematical prerequisite, namely the scalar product of two vectors.
We have learnt about vectors and their use in Chapter 4. Physical quantities like displacement, velocity, acceleration, force etc. are vectors. We have also learnt how vectors are added or subtracted. We now need to know how vectors are multiplied. There are two ways of multiplying vectors which we shall come across : one way known as the scalar product gives a scalar from two vectors and the other known as the vector product produces a new vector from two vectors. We shall look at the vector product in Chapter 7. Here we take up the scalar product of two vectors. The scalar product or dot product of any two vectors A and B, denoted as A.B (read A dot B) is defined as
A.B = A B cos θ (6.1a)
where θ is the angle between the two vectors as shown in Fig. 6.1(a). Since A, B and cos θ are scalars, the dot product of A and B is a scalar quantity. Each vector, A and B, has a direction but their scalar product does not have a direction.
From Eq. (6.1a), we have
A.B = A (B cos θ )
= B (A cos θ )
Geometrically, B cos θ is the projection of B onto A in Fig.6.1 (b) and A cos θ is the projection of A onto B in Fig. 6.1 (c). So, A.B is the product of the magnitude of A and the component of B along A. Alternatively, it is the product of the magnitude of B and the component of A along B.
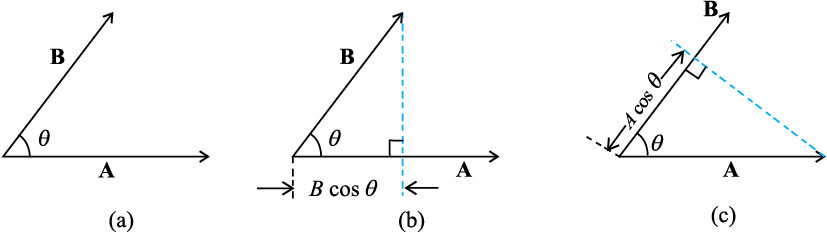
Fig. 6.1 (a) The scalar product of two vectors A and B is a scalar : A.B = A B cos θ. (b) Bcos θ is the projection of B onto A. (c) A cos θ is the projection of A onto B.
Equation (6.1a) shows that the scalar product follows the commutative law :
A.B = B.A
Scalar product obeys the distributive law:
A. (B + C) = A.B + A.C
Further, A. (λ B) = λ (A.B)
where λ is a real number.
The proofs of the above equations are left to you as an exercise.
For unit vectors 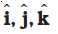 we have
we have
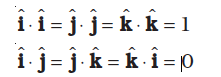
Given two vectors
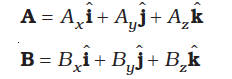
their scalar product is
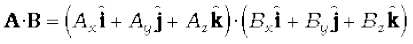
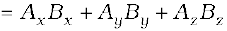
From the definition of scalar product and (Eq. 6.1b) we have :
( i ) 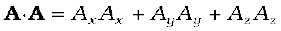
Or, 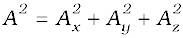
since A.A = |A ||A| cos 0 = A2.
(ii) A.B = 0, if A and B are perpendicular.
Example 6.1 Find the angle between force F = 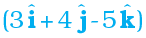 unit and displacement d =
unit and displacement d = 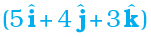 unit. Also find the projection of F on d.
unit. Also find the projection of F on d.
Answer F.d =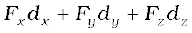
= 3 (5) + 4 (4) + (– 5) (3)
= 16 unit
Hence F.d = 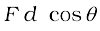 = 16 unit
= 16 unit
Now F.F = 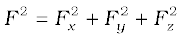
= 9 + 16 + 25
= 50 unit
and d.d = d2 = 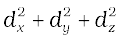
= 25 + 16 + 9
= 50 unit
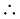 cos θ =
cos θ = 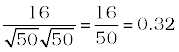 ,
,
θ = cos–1 0.32
The following relation for rectilinear motion under constant acceleration a has been encountered in Chapter 3,
v2 − u2 = 2 as (6.2)
where u and v are the initial and final speeds and s the distance traversed. Multiplying both sides by m/2, we have
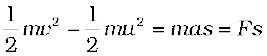
where the last step follows from Newton’s Second Law. We can generalise Eq. (6.2) to three dimensions by employing vectors
v2 − u2 = 2 a.d
Here a and d are acceleration and displacement vectors of the object respectively.
Once again multiplying both sides by m/2 , we obtain
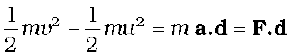
The above equation provides a motivation for the definitions of work and kinetic energy. The left side of the equation is the difference in the quantity ‘half the mass times the square of the speed’ from its initial value to its final value. We call each of these quantities the ‘kinetic energy’, denoted by K. The right side is a product of the displacement and the component of the force along the displacement. This quantity is called ‘work’ and is denoted by W. Eq. (6.2b) is then
Kf − Ki = W (6.3)
where Ki and Kf are respectively the initial and final kinetic energies of the object. Work refers to the force and the displacement over which it acts. Work is done by a force on the body over a certain displacement.
Equation (6.2) is also a special case of the work-energy (WE) theorem : The change in kinetic energy of a particle is equal to the work done on it by the net force. We shall generalise the above derivation to a varying force in a later section.
Example 6.2 It is well known that a raindrop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop but is otherwise undetermined. Consider a drop of mass 1.00 g falling from a height 1.00 km. It hits the ground with a speed of 50.0 m s-1. (a) What is the work done by the gravitational force ? What is the work done by the unknown resistive force?
Answer (a) The change in kinetic energy of the drop is
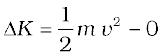
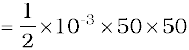
= 1.25 J
where we have assumed that the drop is initially at rest.
Assuming that g is a constant with a value 10 m/s2, the work done by the gravitational force is,
Wg = mgh
= 10-3 ×10 ×103
= 10.0 J
(b) From the work-energy theorem
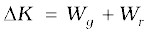
where Wr is the work done by the resistive force on the raindrop. Thus
Wr = ∆K − Wg
= 1.25 −10
= − 8.75 J
is negative.
As seen earlier, work is related to force and the displacement over which it acts. Consider a constant force F acting on an object of mass m. The object undergoes a displacement d in the positive x-direction as shown in Fig. 6.2.
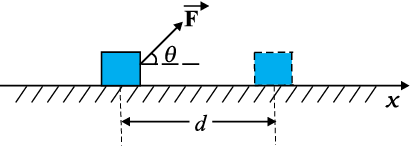
Fig. 6.2 An object undergoes a displacement d under the influence of the force F.
The work done by the force is defined to be the product of component of the force in the direction of the displacement and the magnitude of this displacement. Thus
W = (F cos θ )d = F.d (6.4)
We see that if there is no displacement, there is no work done even if the force is large. Thus, when you push hard against a rigid brick wall, the force you exert on the wall does no work. Yet your muscles are alternatively contracting and relaxing and internal energy is being used up and you do get tired. Thus, the meaning of work in physics is different from its usage in everyday language.
No work is done if :
(i) the displacement is zero as seen in the example above. A weightlifter holding a 150 kg mass steadily on his shoulder for 30 s does no work on the load during this time.
(ii) the force is zero. A block moving on a smooth horizontal table is not acted upon by a horizontal force (since there is no friction), but may undergo a large displacement.
(iii) the force and displacement are mutually perpendicular. This is so since, for θ = π/2 rad (= 90o), cos (π/2) = 0. For the block moving on a smooth horizontal table, the gravitational force mg does no work since it acts at right angles to the displacement. If we assume that the moon’s orbits around the earth is perfectly circular then the earth’s gravitational force does no work. The moon’s instantaneous displacement is tangential while the earth’s force is radially inwards and θ = π/2.
Work can be both positive and negative. If θ is between 0o and 90o, cos θ in Eq. (6.4) is positive. If θ is between 90o and 180o, cos θ is negative. In many examples the frictional force opposes displacement and θ = 180o. Then the work done by friction is negative (cos 180o = –1).
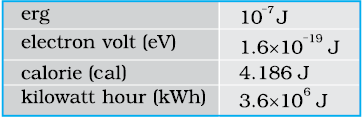
From Eq. (6.4) it is clear that work and energy have the same dimensions, [ML2T–2]. The SI unit of these is joule (J), named after the famous British physicist James Prescott Joule (1811-1869). Since work and energy are so widely used as physical concepts, alternative units abound and some of these are listed in Table 6.1.
Example 6.3 A cyclist comes to a skidding stop in 10 m. During this process, the force on the cycle due to the road is 200 N and is directly opposed to the motion. (a) How much work does the road do on the cycle ? (b) How much work does the cycle do on the road ?
Answer Work done on the cycle by the road is the work done by the stopping (frictional) force on the cycle due to the road.
(a) The stopping force and the displacement make an angle of 180o (π rad) with each other. Thus, work done by the road,
Wr = Fd cosθ
= 200 × 10 × cos π
= – 2000 J
It is this negative work that brings the cycle to a halt in accordance with WE theorem.
(b) From Newton’s Third Law an equal and opposite force acts on the road due to the cycle. Its magnitude is 200 N. However, the road undergoes no displacement. Thus, work done by cycle on the road is zero.
The lesson of Example 6.3 is that though the force on a body A exerted by the body B is always equal and opposite to that on B by A (Newton’s Third Law); the work done on A by B is not necessarily equal and opposite to the work done on B by A.
As noted earlier, if an object of mass m has velocity v, its kinetic energy K is
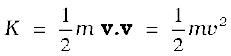
Kinetic energy is a scalar quantity. The kinetic energy of an object is a measure of the work an object can do by the virtue of its motion. This notion has been intuitively known for a long time. The kinetic energy of a fast flowing stream has been used to grind corn. Sailing ships employ the kinetic e
nergy of the wind. Table 6.2 lists the kinetic energies for various objects.
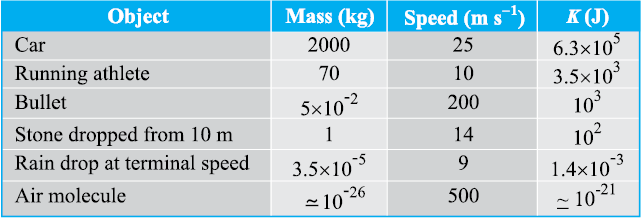
Example 6.4 In a ballistics demonstration a police officer fires a bullet of mass 50.0 g with speed 200 m s-1 (see Table 6.2) on soft plywood of thickness 2.00 cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet ?
Answer The initial kinetic energy of the bullet is mv2/2 = 1000 J. It has a final kinetic energy of 0.1×1000 = 100 J. If vf is the emergent speed of the bullet,
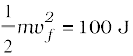
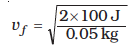
= 63.2 m s–1
The speed is reduced by approximately 68% (not 90%).
A constant force is rare. It is the variable force, which is more commonly encountered. Fig. 6.3 is a plot of a varying force in one dimension.
If the displacement ∆x is small, we can take the force F(x) as approximately constant and the work done is then
∆W =F(x) ∆x
This is illustrated in Fig. 6.3(a). Adding successive rectangular areas in Fig. 6.3(a) we get the total work done as
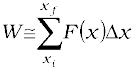
where the summation is from the initial position xi to the final position xf.
If the displacements are allowed to approach zero, then the number of terms in the sum increases without limit, but the sum approaches a definite value equal to the area under the curve in Fig. 6.3(b). Then the work done is
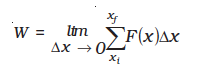
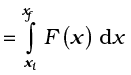
where ‘lim’ stands for the limit of the sum when ∆x tends to zero. Thus, for a varying force
the work done can be expressed as a definite integral of force over displacement (see also Appendix 3.1).
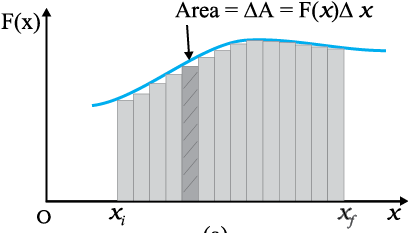 Fig. 6.3(a)
Fig. 6.3(a)
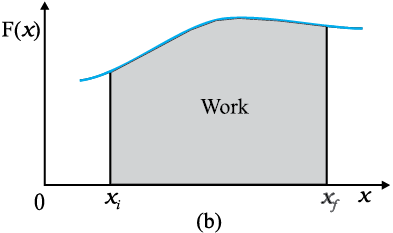
Fig. 6.3 (a) The shaded rectangle represents the work done by the varying force F(x), over the small displacement ∆x, ∆W = F(x) ∆x.
(b) adding the areas of all the rectangles we find that for ∆x → 0, the area under the curve is exactly equal to the work done by F(x).
Example 6.5 A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m. Plot the force applied by the woman and the frictional force, which is 50 N versus displacement. Calculate the work done by the two forces over 20 m.
Answer
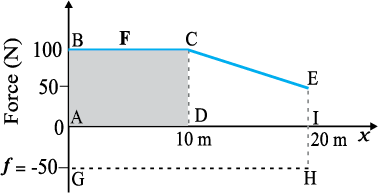
Fig. 6.4 Plot of the force F applied by the woman and the opposing frictional force f versus displacement.
The plot of the applied force is shown in Fig. 6.4. At x = 20 m, F = 50 N (≠ 0). We are given that the frictional force f is |f|= 50 N. It opposes motion and acts in a direction opposite to F. It is therefore, shown on the negative side of the force axis.
The work done by the woman is
WF → area of the rectangle ABCD + area of the trapezium CEID
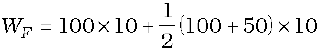
= 1000 + 750
= 1750 J
The work done by the frictional force is
Wf → area of the rectangle AGHI
Wf = (−50) × 20
= − 1000 J
The area on the negative side of the force axis has a negative sign.
We are now familiar with the concepts of work and kinetic energy to prove the work-energy theorem for a variable force. We confine ourselves to one dimension. The time rate of change of kinetic energy is
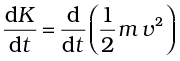
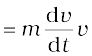
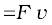 (from Newton’s Second Law)
(from Newton’s Second Law)
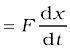
Thus
dK = Fdx
Integrating from the initial position (x i ) to final position ( x f ), we have
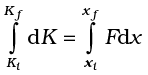
where, Ki and K f are the initial and final kinetic energies corresponding to x i and x f.
or 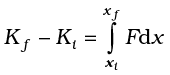
From Eq. (6.7), it follows that
Kf − Ki = W (6.8b)
Thus, the WE theorem is proved for a variable force.
While the WE theorem is useful in a variety of problems, it does not, in general, incorporate the complete dynamical information of Newton’s second law. It is an integral form of Newton’s second law. Newton’s second law is a relation between acceleration and force at any instant of time. Work-energy theorem involves an integral over an interval of time. In this sense, the temporal (time) information contained in the statement of Newton’s second law is ‘integrated over’ and is not available explicitly. Another observation is that Newton’s second law for two or three dimensions is in vector form whereas the work-energy theorem is in scalar form. In the scalar form, information with respect to directions contained in Newton’s second law is not present.
Example 6.6 A block of mass m = 1 kg, moving on a horizontal surface with speed vi = 2 m s–1 enters a rough patch ranging from x = 0.10 m to x = 2.01 m. The retarding force Fr on the block in this range is inversely proportional to x over this range,
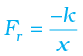 for 0.1 < x < 2.01 m
for 0.1 < x < 2.01 m
= 0 for x < 0.1m and x > 2.01 m
where k = 0.5 J. What is the final kinetic energy and speed vf of the block as it crosses this patch ?
Answer From Eq. (6.8a)
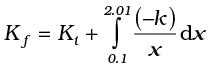
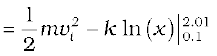
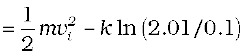
= 2 − 0.5 ln (20.1)
= 2 − 1.5 = 0.5 J
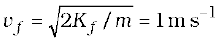
Here, note that ln is a symbol for the natural logarithm to the base e and not the logarithm to the base 10 [ln X = loge X = 2.303 log10 X].
The word potential suggests possibility or capacity for action. The term potential energy brings to one’s mind ‘stored’ energy. A stretched bow-string possesses potential energy. When it is released, the arrow flies off at a great speed. The earth’s crust is not uniform, but has discontinuities and dislocations that are called fault lines. These fault lines in the earth’s crust are like ‘compressed springs’. They possess a large amount of potential energy. An earthquake results when these fault lines readjust. Thus, potential energy is the ‘stored energy’ by virtue of the position or configuration of a body. The body left to itself releases this stored energy in the form of kinetic energy. Let us make our notion of potential energy more concrete.
The gravitational force on a ball of mass m is mg . g may be treated as a constant near the earth surface. By ‘near’ we imply that the height h of the ball above the earth’s surface is very small compared to the earth’s radius RE (h <
V (h) = mgh
If h is taken as a variable, it is easily seen that the gravitational force F equals the negative of the derivative of V(h) with respect to h. Thus,
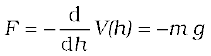
The negative sign indicates that the gravitational force is downward. When released, the ball comes down with an increasing speed. Just before it hits the ground, its speed is given by the kinematic relation,
v2 = 2gh
This equation can be written as
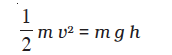
which shows that the gravitational potential energy of the object at height h, when the object is released, manifests itself as kinetic energy of the object on reaching the ground.
* The variation of g with height is discussed in Chapter 8 on Gravitation.
Physically, the notion of potential energy is applicable only to the class of forces where work done against the force gets ‘stored up’ as energy. When external constraints are removed, it manifests itself as kinetic energy. Mathematically, (for simplicity, in one dimension) the potential energy V(x) is defined if the force F(x) can be written as
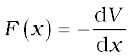
This implies that
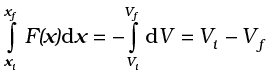
The work done by a conservative force such as gravity depends on the initial and final positions only. In the previous chapter we have worked on examples dealing with
inclined planes. If an object of mass m is released from rest, from the top of a smooth (frictionless) inclined plane of height h, its speed at the bottom is
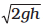 irrespective of the angle of inclination. Thus, at the bottom of the inclined plane it acquires a kinetic energy, mgh. If the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object, the force would be called non-conservative.
irrespective of the angle of inclination. Thus, at the bottom of the inclined plane it acquires a kinetic energy, mgh. If the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object, the force would be called non-conservative.
The dimensions of potential energy are [ML2T –2] and the unit is joule (J), the same as kinetic energy or work. To reiterate, the change in potential energy, for a conservative force, ∆V is equal to the negative of the work done by the force
∆V = − F(x) ∆x (6.9)
In the example of the falling ball considered in this section we saw how potential energy was converted to kinetic energy. This hints at an important principle of conservation in mechanics, which we now proceed to examine.
For simplicity, we demonstrate this important principle for one-dimensional motion. Suppose that a body undergoes displacement ∆x under the action of a conservative force F. Then from the WE theorem we have,
∆K = F(x) ∆x
If the force is conservative, the potential energy function V(x) can be defined such that
− ∆V = F(x) ∆x
The above equations imply that
∆K + ∆V = 0
∆(K + V ) = 0 (6.10)
which means that K + V, the sum of the kinetic and potential energies of the body is a constant. Over the whole path, xi to xf, this means that
Ki + V(xi ) = Kf + V(xf ) (6.11)
The quantity K +V(x), is called the total mechanical energy of the system. Individually the kinetic energy K and the potential energy V(x) may vary from point to point, but the sum is a constant. The aptness of the term ‘conservative force’ is now clear.
Let us consider some of the definitions of a conservative force.
W = Kf – Ki = V (xi ) – V(xf )
which depends on the end points.
Thus, the principle of conservation of total mechanical energy can be stated as
The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.
The above discussion can be made more concrete by considering the example of the gravitational force once again and that of the spring force in the next section. Fig. 6.5 depicts a ball of mass m being dropped from a cliff of height H.
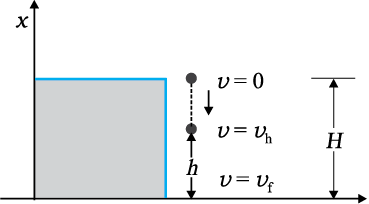
Fig. 6.5 The conversion of potential energy to kinetic energy for a ball of mass m dropped from a height H.
The total mechanical energies E0, Eh, and EH of the ball at the indicated heights zero (ground level), h and H, are
EH = mgH (6.11 a)
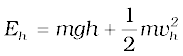
E0 = (1/2) mvf2 (6.11 c)
The constant force is a special case of a spatially dependent force F(x). Hence, the mechanical energy is conserved. Thus
EH = E0
or, 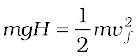
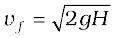
a result that was obtained in section 3.7 for a freely falling body.
Further,
EH = Eh
which implies,
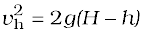
and is a familiar result from kinematics.
At the height H, the energy is purely potential. It is partially converted to kinetic at height h and is fully kinetic at ground level. This illustrates the conservation of mechanical energy.
Example 6.7 A bob of mass m is suspended by a light string of length L . It is imparted a horizontal velocity vo at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for (i) vo; (ii) the speeds at points B and C; (iii) the ratio of the kinetic energies (KB/KC) at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
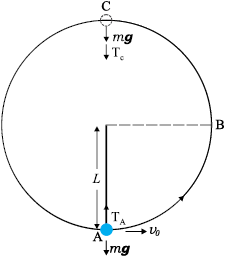
Fig. 6.6
Answer (i) There are two external forces on the bob : gravity and the tension (T) in the string. The latter does no work since the displacement of the bob is always normal to the string. The potential energy of the bob is thus associated with the gravitational force only. The total mechanical energy E of the system is conserved. We take the potential energy of the system to be zero at the lowest point A. Thus, at A :
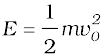
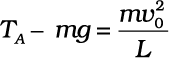 [Newton’s Second Law]
[Newton’s Second Law]
where TA is the tension in the string at A. At the highest point C, the string slackens, as the tension in the string (TC) becomes zero.
Thus, at C
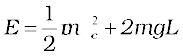
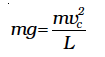
[Newton’s Second Law] (6.14)
where vC is the speed at C. From Eqs. (6.13) and (6.14)
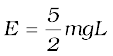
Equating this to the energy at A
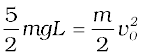
or, 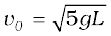
(ii) It is clear from Eq. (6.14)
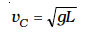
At B, the energy is
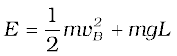
Equating this to the energy at A and employing the result from (i), namely
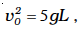
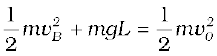
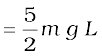
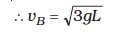
(iii) The ratio of the kinetic energies at B and C is :
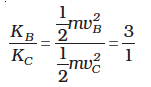
At point C, the string becomes slack and the velocity of the bob is horizontal and to the left. If the connecting string is cut at this instant, the bob will execute a projectile motion with horizontal projection akin to a rock kicked horizontally from the edge of a cliff. Otherwise the bob will continue on its circular path and complete the revolution.
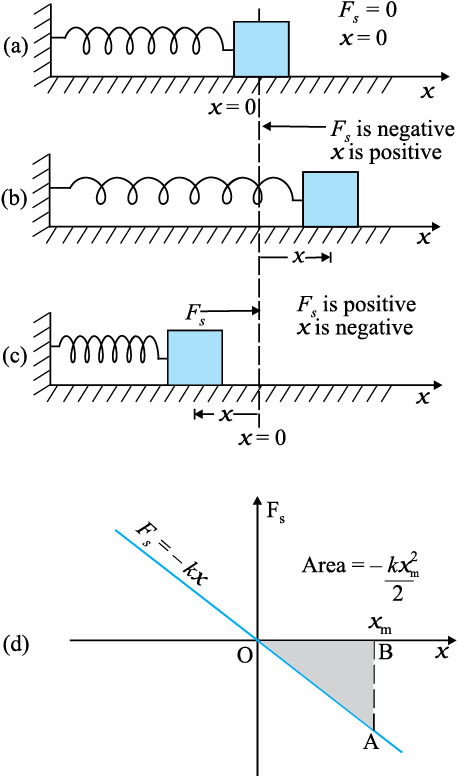
The spring force is an example of a variable force which is conservative. Fig. 6.7 shows a block attached to a spring and resting on a smooth horizontal surface. The other end of the spring is attached to a rigid wall. The spring is light and may be treated as massless. In an ideal spring, the spring force Fs is proportional to x where x is the displacement of the block from the equilibrium position. The displacement could be either positive [Fig. 6.7(b)] or negative [Fig. 6.7(c)]. This force law for the spring is called Hooke’s law and is mathematically stated as
Fs = − kx
The constant k is called the spring constant. Its unit is N m-1. The spring is said to be stiff if k is large and soft if k is small.
Suppose that we pull the block outwards as in Fig. 6.7(b). If the extension is xm, the work done by the spring force is
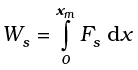
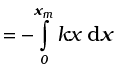
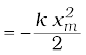
This expression may also be obtained by considering the area of the triangle as in Fig. 6.7(d). Note that the work done by the external pulling force F is positive since it overcomes the spring force.
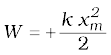
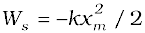
The same is true when the spring is compressed with a displacement xc (< 0). The spring force does work
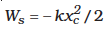
while the external force F does work 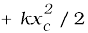 . If the block is moved from an initial displacement xi to a final displacement xf , the work done by the spring force Ws is
. If the block is moved from an initial displacement xi to a final displacement xf , the work done by the spring force Ws is
.
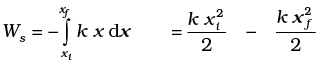
Thus the work done by the spring force depends only on the end points. Specifically, if the block is pulled from xi and allowed to return to xi ; 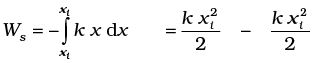
= 0 (6.18)
The work done by the spring force in a cyclic process is zero. We have explicitly demonstrated that the spring force (i) is position dependent only as first stated by Hooke, (Fs = − kx); (ii) does work which only depends on the initial and final positions, e.g. Eq. (6.17). Thus, the spring force is a conservative force.
We define the potential energy V(x) of the spring to be zero when block and spring system is in the equilibrium position. For an extension (or compression) x the above analysis suggests that
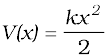
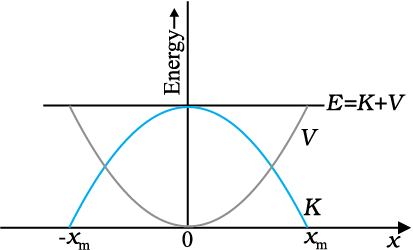
You may easily verify that − dV/dx = − k x, the spring force. If the block of mass m in Fig. 6.7 is extended to xm and released from rest, then its total mechanical energy at any arbitrary point x, where x lies between – xm and + xm, will be given by
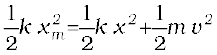
where we have invoked the conservation of mechanical energy. This suggests that the speed and the kinetic energy
will be maximum at the equilibrium position, x = 0, i.e.,
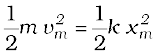
where vm is the maximum speed.
or 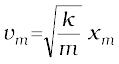
Note that k/m has the dimensions of [T-2] and our equation is dimensionally correct. The kinetic energy gets converted to potential energy and vice versa, however, the total mechanical energy remains constant. This is graphically depicted in Fig. 6.8.
Example 6.8 To simulate car accidents, auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000 kg moving with a speed 18.0 km/h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25 × 103 N m–1. What is the maximum compression of the spring ?
Answer At maximum compression the kinetic energy of the car is converted entirely into the potential energy of the spring.
The kinetic energy of the moving car is
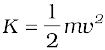
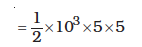
K = 1.25 × 104 J
where we have converted 18 km h–1 to 5 m s–1 [It is useful to remember that 36 km h–1 = 10 m s–1]. At maximum compression xm, the potential energy V of the spring is equal to the kinetic energy K of the moving car from the principle of conservation of mechanical energy.
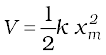
= 1.25 × 104 J
We obtain
xm = 2.00 m
We note that we have idealised the situation. The spring is considered to be massless. The surface has been considered to possess negligible friction.
We conclude this section by making a few remarks on conservative forces.
(i) Information on time is absent from the above discussions. In the example considered above, we can calculate the compression, but not the time over which the compression occurs. A solution of Newton’s Second Law for this system is required for temporal information.
(ii) Not all forces are conservative. Friction, for example, is a non-conservative force. The principle of conservation of energy will have to be modified in this case. This is illustrated in Example 6.9.
(iii) The zero of the potential energy is arbitrary. It is set according to convenience. For the spring force we took V(x) = 0, at x = 0, i.e. the unstretched spring had zero potential energy. For the constant gravitational force mg, we took V = 0 on the earth’s surface. In a later chapter we shall see that for the force due to the universal law of gravitation, the zero is best defined at an infinite distance from the gravitational source. However, once the zero of the potential energy is fixed in a given discussion, it must be consistently adhered to throughout the discussion. You cannot change horses in midstream !
Example 6.9 Consider Example 6.8 taking the coefficient of friction, µ, to be 0.5 and calculate the maximum compression of the spring.
Answer In presence of friction, both the spring force and the frictional force act so as to oppose the compression of the spring as shown in Fig. 6.9.
We invoke the work-energy theorem, rather than the conservation of mechanical energy.
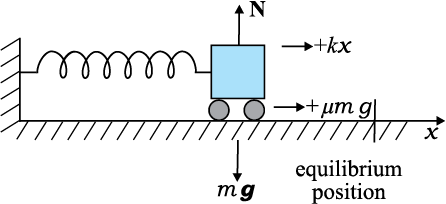
Fig. 6.9 The forces acting on the car.
The change in kinetic energy is
∆K = Kf − Ki 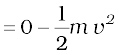
The work done by the net force is
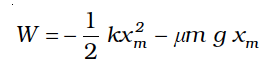
Equating we have
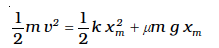
Now µmg = 0.5 × 103 × 10 = 5 × 103 N (taking g =10.0 m s-2). After rearranging the above equation we obtain the following quadratic equation in the unknown xm.
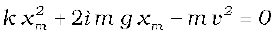
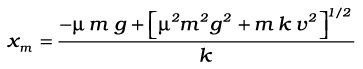
where we take the positive square root since xm is positive. Putting in numerical values we obtain
xm = 1.35 m
which, as expected, is less than the result in Example 6.8.
If the two forces on the body consist of a conservative force Fc and a non-conservative force Fnc , the conservation of mechanical energy formula will have to be modified. By the WE theorem
(Fc+ Fnc ) ∆x = ∆K
But Fc ∆x = − ∆V
Hence, ∆(K + V) = Fnc ∆x
∆E = Fnc ∆x
where E is the total mechanical energy. Over the path this assumes the form
Ef − Ei = Wnc
where Wnc is the total work done by the non-conservative forces over the path. Note that unlike the conservative force, Wnc depends on the particular path i to f.
In the previous section we have discussed mechanical energy. We have seen that it can be classified into two distinct categories : one based on motion, namely kinetic energy; the other on configuration (position), namely potential energy. Energy comes in many a forms which transform into one another in ways which may not often be clear to us.
We have seen that the frictional force is not a conservative force. However, work is associated with the force of friction, Example 6.5. A block of mass m sliding on a rough horizontal surface with speed v0 comes to a halt over a distance x0. The work done by the force of kinetic friction f over x0 is –f x0. By the work-energy theorem 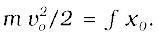 If we confine our scope to mechanics, we would say that the kinetic energy of the block is ‘lost’ due to the frictional force. On examination of the block and the table we would detect a slight increase in their temperatures. The work done by friction is not ‘lost’, but is transferred as heat energy. This raises the internal energy of the block and the table. In winter, in order to feel warm, we generate heat by vigorously rubbing our palms together. We shall see later that the internal energy is associated with the ceaseless, often random, motion of molecules. A quantitative idea of the transfer of heat energy is obtained by noting that 1 kg of water releases about 42000 J of energy when it cools by10 °C.
If we confine our scope to mechanics, we would say that the kinetic energy of the block is ‘lost’ due to the frictional force. On examination of the block and the table we would detect a slight increase in their temperatures. The work done by friction is not ‘lost’, but is transferred as heat energy. This raises the internal energy of the block and the table. In winter, in order to feel warm, we generate heat by vigorously rubbing our palms together. We shall see later that the internal energy is associated with the ceaseless, often random, motion of molecules. A quantitative idea of the transfer of heat energy is obtained by noting that 1 kg of water releases about 42000 J of energy when it cools by10 °C.
One of the greatest technical achievements of humankind occurred when we discovered how to ignite and control fire. We learnt to rub two flint stones together (mechanical energy), got them to heat up and to ignite a heap of dry leaves (chemical energy), which then provided sustained warmth. A matchstick ignites into a bright flame when struck against a specially prepared chemical surface. The lighted matchstick, when applied to a firecracker, results in a spectacular display of sound and light.
Chemical energy arises from the fact that the molecules participating in the chemical reaction have different binding energies. A stable chemical compound has less energy than the separated parts. A chemical reaction is basically a rearrangement of atoms. If the total energy of the reactants is more than the products of the reaction, heat is released and the reaction is said to be an exothermic reaction. If the reverse is true, heat is absorbed and the reaction is endothermic. Coal consists of carbon and a kilogram of it when burnt releases about 3 × 107 J of energy.
Chemical energy is associated with the forces that give rise to the stability of substances. These forces bind atoms into molecules, molecules into polymeric chains, etc. The chemical energy arising from the combustion of coal, cooking gas, wood and petroleum is indispensable to our daily existence.
The flow of electrical current causes bulbs to glow, fans to rotate and bells to ring. There are laws governing the attraction and repulsion of charges and currents, which we shall learn later. Energy is associated with an electric current. An urban Indian household consumes about 200 J of energy per second on an average.
Till the end of the nineteenth century, physicists believed that in every physical and chemical process, the mass of an isolated system is conserved. Matter might change its phase, e.g. glacial ice could melt into a gushing stream, but matter is neither created nor destroyed; Albert Einstein (1879-1955) however, showed that mass and energy are equivalent and are related by the relation
E = m c2 (6.20)
where c, the speed of light in vacuum is approximately 3 ×108 m s–1. Thus, a staggering amount of energy is associated with a mere kilogram of matter
E = 1× (3 ×108)2 J = 9 ×1016 J.
This is equivalent to the annual electrical output of a large (3000 MW) power generating station.
The most destructive weapons made by man, the fission and fusion bombs are manifestations of the above equivalence of mass and energy [Eq. (6.20)]. On the other hand the explanation of the life-nourishing energy output of the sun is also based on the above equation. In this case effectively four light hydrogen nuclei fuse to form a helium nucleus whose mass is less than the sum of the masses of the reactants. This mass difference, called the mass defect ∆m is the source of energy (∆m)c2. In fission, a heavy nucleus like uranium 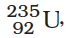 , is split by a neutron into lighter nuclei. Once again the final mass is less than the initial mass and the mass difference translates into energy, which can be tapped to provide electrical energy as in nuclear power plants (controlled nuclear fission) or can be employed in making nuclear weapons (uncontrolled nuclear fission). Strictly, the energy ∆E released in a chemical reaction can also be related to the mass defect ∆m = ∆E/c2. However, for a chemical reaction, this mass defect is much smaller than for a nuclear reaction. Table 6.3 lists the total energies for a variety of events and phenomena.
, is split by a neutron into lighter nuclei. Once again the final mass is less than the initial mass and the mass difference translates into energy, which can be tapped to provide electrical energy as in nuclear power plants (controlled nuclear fission) or can be employed in making nuclear weapons (uncontrolled nuclear fission). Strictly, the energy ∆E released in a chemical reaction can also be related to the mass defect ∆m = ∆E/c2. However, for a chemical reaction, this mass defect is much smaller than for a nuclear reaction. Table 6.3 lists the total energies for a variety of events and phenomena.
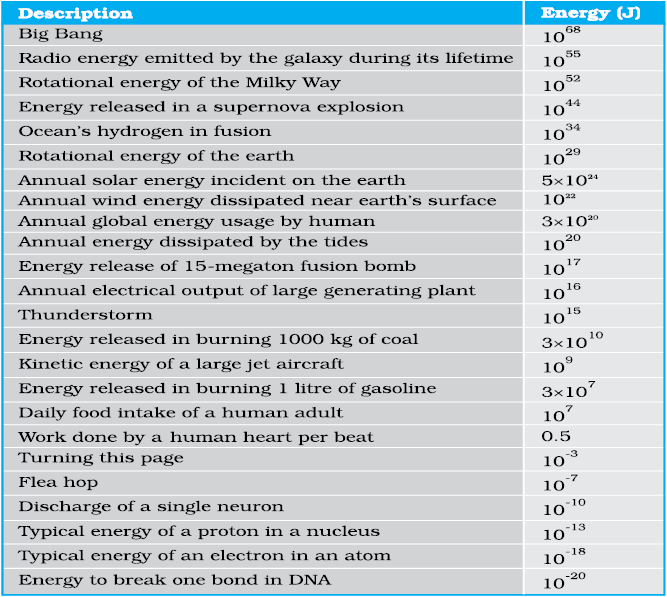
Example 6.10 Examine Tables 6.1-6.3 and express (a) The energy required to break one bond in DNA in eV; (b) The kinetic energy of an air molecule (10—21 J) in eV; (c) The daily intake of a human adult in kilocalories.
Answer (a) Energy required to break one bond of DNA is
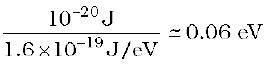
Note 0.1 eV = 100 meV (100 millielectron volt).
(b) The kinetic energy of an air molecule is
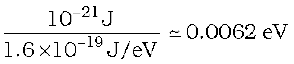
This is the same as 6.2 meV.
(c) The average human consumption in a day is
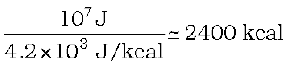
We point out a common misconception created by newspapers and magazines. They mention food values in calories and urge us to restrict diet intake to below 2400 calories. What they should be saying is kilocalories (kcal) and not calories. A person consuming 2400 calories a day will soon starve to death! 1 food calorie is 1 kcal.
We have seen that the total mechanical energy of the system is conserved if the forces doing work on it are conservative. If some of the forces involved are non-conservative, part of the mechanical energy may get transformed into other forms such as heat, light and sound. However, the total energy of an isolated system does not change, as long as one accounts for all forms of energy. Energy may be transformed from one form to another but the total energy of an isolated system remains constant. Energy can neither be created, nor destroyed.
Since the universe as a whole may be viewed as an isolated system, the total energy of the universe is constant. If one part of the universe loses energy, another part must gain an equal amount of energy.
The principle of conservation of energy cannot be proved. However, no violation of this principle has been observed. The concept of conservation and transformation of energy into various forms links together various branches of physics, chemistry and life sciences. It provides a unifying, enduring element in our scientific pursuits. From engineering point of view all electronic, communication and mechanical devices rely on some forms of energy transformation.
Often it is interesting to know not only the work done on an object, but also the rate at which this work is done. We say a person is physically fit if he not only climbs four floors of a building but climbs them fast. Power is defined as the time rate at which work is done or energy is transferred.
The average power of a force is defined as the ratio of the work, W, to the total time t taken
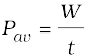
The instantaneous power is defined as the limiting value of the average power as time interval approaches zero,
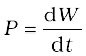
The work dW done by a force F for a displacement dr is dW = F.dr. The instantaneous power can also be expressed as
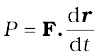
= F.v (6.22)
where v is the instantaneous velocity when the force is F.
Power, like work and energy, is a scalar quantity. Its dimensions are [ML2T–3]. In the SI, its unit is called a watt (W). The watt is 1 J s–1. The unit of power is named after James Watt, one of the innovators of the steam engine in the eighteenth century.
There is another unit of power, namely the horse-power (hp)
1 hp = 746 W
This unit is still used to describe the output of automobiles, motorbikes, etc.
We encounter the unit watt when we buy electrical goods such as bulbs, heaters and refrigerators. A 100 watt bulb which is on for 10 hours uses 1 kilowatt hour (kWh) of energy.
100 (watt) × 10 (hour)
= 1000 watt hour
=1 kilowatt hour (kWh)
= 103 (W) × 3600 (s)
= 3.6 × 106 J
Our electricity bills carry the energy consumption in units of kWh. Note that kWh is a unit of energy and not of power.
Example 6.11 An elevator can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of 2ms–1. The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horse power.
Answer The downward force on the elevator is
F = m g + Ff = (1800 × 10) + 4000 = 22000 N
The motor must supply enough power to balance this force. Hence,
P = F. v = 22000 × 2 = 44000 W = 59 hp
In physics we study motion (change in position). At the same time, we try to discover physical quantities, which do not change in a physical process. The laws of momentum and energy conservation are typical examples. In this section we shall apply these laws to a commonly encountered phenomena, namely collisions. Several games such as billiards, marbles or carrom involve collisions.We shall study the collision of two masses in an idealised form.
Consider two masses m1 and m2. The particle m1 is moving with speed v1i , the subscript ‘i’ implying initial. We can consider m2 to be at rest. No loss of generality is involved in making such a selection. In this situation the mass m1 collides with the stationary mass m2 and this is depicted in Fig. 6.10.
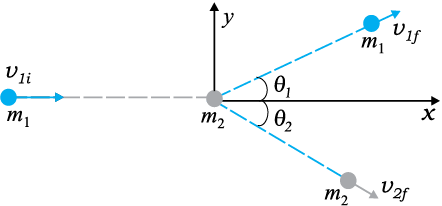
Fig. 6.10 Collision of mass m1, with a stationary mass m2.
The masses m1 and m2 fly-off in different directions. We shall see that there are relationships, which connect the masses, the velocities and the angles.
In all collisions the total linear momentum is conserved; the initial momentum of the system is equal to the final momentum of the system. One can argue this as follows. When two objects collide, the mutual impulsive forces acting over the collision time ∆t cause a change in their respective momenta :
∆p1 = F12 ∆t
∆p2 = F21 ∆t
where F12 is the force exerted on the first particle by the second particle. F21 is likewise the force exerted on the second particle by the first particle. Now from Newton’s third law, F12 = − F21. This implies
∆p1 + ∆p2 = 0
The above conclusion is true even though the forces vary in a complex fashion during the collision time ∆t. Since the third law is true at every instant, the total impulse on the first object is equal and opposite to that on the second.
On the other hand, the total kinetic energy of the system is not necessarily conserved. The impact and deformation during collision may generate heat and sound. Part of the initial kinetic energy is transformed into other forms of energy. A useful way to visualise the deformation during collision is in terms of a ‘compressed spring’. If the ‘spring’ connecting the two masses regains its original shape without loss in energy, then the initial kinetic energy is equal to the final kinetic energy but the kinetic energy during the collision time ∆t is not constant. Such a collision is called an elastic collision. On the other hand the deformation may not be relieved and the two bodies could move together after the collision. A collision in which the two particles move together after the collision is called a completely inelastic collision. The intermediate case where the deformation is partly relieved and some of the initial kinetic energy is lost is more common and is appropriately called an inelastic collision.
Consider first a completely inelastic collision in one dimension. Then, in Fig. 6.10,
θ 1 = θ 2 = 0
m1v1i = (m1+m2)vf (momentum conservation)
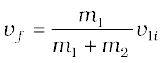
The loss in kinetic energy on collision is
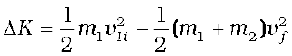
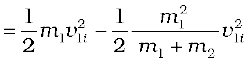 [using Eq. (6.23)]
[using Eq. (6.23)]
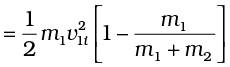
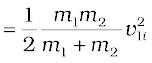
which is a positive quantity as expected.
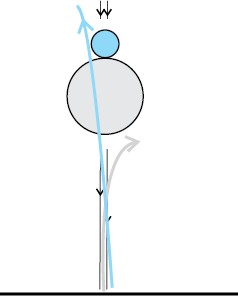
In performing an experiment on collision on a horizontal surface, we face three difficulties. One, there will be friction and bodies will not travel with uniform velocities. Two, if two bodies of different sizes collide on a table, it would be difficult to arrange them for a head-on collision unless their centres of mass are at the same height above the surface. Three, it will be fairly difficult to measure velocities of the two bodies just before and just after collision.
By performing this experiment in a vertical direction, all the three difficulties vanish. Take two balls, one of which is heavier (basketball/football/volleyball) and the other lighter (tennis ball/rubber ball/table tennis ball). First take only the heavier ball and drop it vertically from some height, say 1 m. Note to which it rises. This gives the velocities near the floor or ground, just before and just after the bounce (by using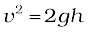 ). Hence you will get the coefficient of restitution.
). Hence you will get the coefficient of restitution.
Now take the big ball and a small ball and hold them in your hands one over the other, with the heavier ball below the lighter one, as shown here. Drop them together, taking care that they remain together while falling, and see what happens. You will find that the heavier ball rises less than when it was dropped alone, while the lighter one shoots up to about 3 m. With practice, you will be able to hold the ball properly so that the lighter ball rises vertically up and does not fly sideways. This is head-on collision.
You can try to find the best combination of balls which gives you the best effect. You can measure the masses on a standard balance. We leave it to you to think how you can determine the initial and final velocities of the balls.
Consider next an elastic collision. Using the above nomenclature with θ1 = θ2 = 0, the momentum and kinetic energy conservation equations are
m1v1i = m1v1f + m2v2f (6.24)
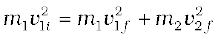
From Eqs. (6.24) and (6.25) it follows that,
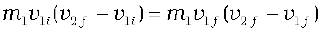
or, 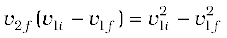
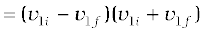
Hence, 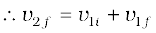
Substituting this in Eq. (6.24), we obtain
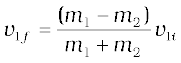
and 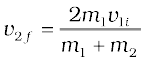
Thus, the ‘unknowns’ {v1f, v2f} are obtained in terms of the ‘knowns’ {m1, m2, v1i}. Special cases of our analysis are interesting.
Case I : If the two masses are equal
v1f = 0
v2f = v1i
The first mass comes to rest and pushes off the second mass with its initial speed on collision.
Case II : If one mass dominates, e.g. m2 > > m1 v1f ~ − v1i v2f ~ 0
The heavier mass is undisturbed while the lighter mass reverses its velocity.
Example 6.12 Slowing down of neutrons: In a nuclear reactor a neutron of high speed (typically 107 m s–1) must be slowed to 103 m s–1 so that it can have a high probability of interacting with isotope  and causing it to fission. Show that a neutron can lose most of its kinetic energy in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a few times the neutron mass. The material making up the light nuclei, usually heavy water (D2O) or graphite, is called a moderator.
and causing it to fission. Show that a neutron can lose most of its kinetic energy in an elastic collision with a light nuclei like deuterium or carbon which has a mass of only a few times the neutron mass. The material making up the light nuclei, usually heavy water (D2O) or graphite, is called a moderator.
Answer The initial kinetic energy of the neutron is
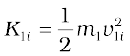
while its final kinetic energy from Eq. (6.27)
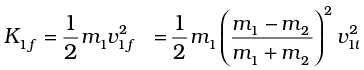
The fractional kinetic energy lost is
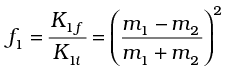
while the fractional kinetic energy gained by the moderating nuclei K2f /K1i is
f2 = 1 − f1 (elastic collision)
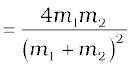
One can also verify this result by substituting from Eq. (6.28).
For deuterium m2 = 2m1 and we obtain f1 = 1/9 while f2 = 8/9. Almost 90% of the neutron’s energy is transferred to deuterium. For carbon f1 = 71.6% and f2 = 28.4%. In practice, however, this number is smaller since head-on collisions are rare.
If the initial velocities and final velocities of both the bodies are along the same straight line, then it is called a one-dimensional collision, or head-on collision. In the case of small spherical bodies, this is possible if the direction of travel of body 1 passes through the centre of body 2 which is at rest. In general, the collision is two-dimensional, where the initial velocities and the final velocities lie in a plane.
Fig. 6.10 also depicts the collision of a moving mass m1 with the stationary mass m2. Linear momentum is conserved in such a collision. Since momentum is a vector this implies three equations for the three directions {x, y, z}. Consider the plane determined by the final velocity directions of m1 and m2 and
choose it to be the x-y plane. The conservation of the z-component of the linear momentum implies that the entire collision is in the x-y plane. The x- and y-component equations are
m1v1i = m1v1f cos θ 1 + m2v2f cos θ 2 (6.29)
0 = m1v1f sin θ1 − m2v2f sin θ2 (6.30)
One knows {m1, m2, v1i} in most situations. There are thus four unknowns {v1f , v2f , θ1 and θ2}, and only two equations. If θ 1 = θ 2 = 0, we regain Eq. (6.24) for one dimensional collision.
If, further the collision is elastic,
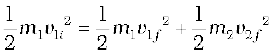
We obtain an additional equation. That still leaves us one equation short. At least one of the four unknowns, say θ 1, must be made known for the problem to be solvable. For example, θ1 can be determined by moving a detector in an angular fashion from the x to the y axis. Given {m1, m2, v1i , θ1} we can determine {v1f , v2f , θ2} from Eqs. (6.29)-(6.31).
Example 6.13 Consider the collision depicted in Fig. 6.10 to be between two billiard balls with equal masses m1 = m2. The first ball is called the cue while the second ball is called the target. The billiard player wants to ‘sink’ the target ball in a corner pocket, which is at an angle θ2 = 37°. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain θ 1.
Answer From momentum conservation, since the masses are equal
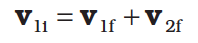
or
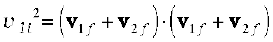
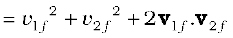
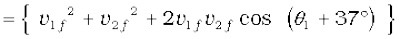
Since the collision is elastic and m1 = m2 it follows from conservation of kinetic energy that 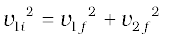
Comparing Eqs. (6.32) and (6.33), we get
cos (θ1 + 37°) = 0
or θ1 + 37° = 90°
Thus, θ1 = 53°
This proves the following result : when two equal masses undergo a glancing elastic collision with one of them at rest, after the collision, they will move at right angles to each other.
The matter simplifies greatly if we consider spherical masses with smooth surfaces, and assume that collision takes place only when the bodies touch each other. This is what happens in the games of marbles, carrom and billiards.
In our everyday world, collisions take place only when two bodies touch each other. But consider a comet coming from far distances to the sun, or alpha particle coming towards a nucleus and going away in some direction. Here we have to deal with forces involving action at a distance. Such an event is called scattering. The velocities and directions in which the two particles go away depend on their initial velocities as well as the type of interaction between them, their masses, shapes and sizes.
1. The work-energy theorem states that the change in kinetic energy of a body is the work done by the net force on the body.
Kf - Ki = Wnet
2. A force is conservative if (i) work done by it on an object is path independent and depends only on the end points {xi, xj}, or (ii) the work done by the force is zero for an arbitrary closed path taken by the object such that it returns to its initial position.
3. For a conservative force in one dimension, we may define a potential energy function V(x) such that
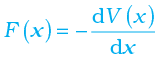
or 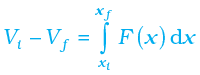
4. The principle of conservation of mechanical energy states that the total mechanical energy of a body remains constant if the only forces that act on the body are conservative.
5. The gravitational potential energy of a particle of mass m at a height x about the earth’s surface is
V(x) = m g x
where the variation of g with height is ignored.
6. The elastic potential energy of a spring of force constant k and extension x is
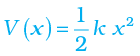
7. The scalar or dot product of two vectors A and B is written as A.B and is a scalar quantity given by : A.B = AB cos θ, where θ is the angle between A and B. It can be positive, negative or zero depending upon the value of θ. The scalar product of two vectors can be interpreted as the product of magnitude of one vector and component of the other vector along the first vector. For unit vectors :
 and
and 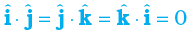
Scalar products obey the commutative and the distributive laws.
1. The phrase ‘calculate the work done’ is incomplete. We should refer (or imply clearly by context) to the work done by a specific force or a group of forces on a given body over a certain displacement.
2. Work done is a scalar quantity. It can be positive or negative unlike mass and kinetic energy which are positive scalar quantities. The work done by the friction or viscous force on a moving body is negative.
3. For two bodies, the sum of the mutual forces exerted between them is zero from Newton’s Third Law,
F12 + F21 = 0
But the sum of the work done by the two forces need not always cancel, i.e.
W12 + W21 ≠ 0
However, it may sometimes be true.
4. The work done by a force can be calculated sometimes even if the exact nature of the force is not known. This is clear from Example 6.2 where the WE theorem is used in such a situation.
5. The WE theorem is not independent of Newton’s Second Law. The WE theorem may be viewed as a scalar form of the Second Law. The principle of conservation of mechanical energy may be viewed as a consequence of the WE theorem for conservative forces.
6. The WE theorem holds in all inertial frames. It can also be extended to non-inertial frames provided we include the pseudoforces in the calculation of the net force acting on the body under consideration.
7. The potential energy of a body subjected to a conservative force is always undetermined upto a constant. For example, the point where the potential energy is zero is a matter of choice. For the gravitational potential energy mgh, the zero of the potential energy is chosen to be the ground. For the spring potential energy kx2/2 , the zero of the potential energy is the equilibrium position of the oscillating mass.
8. Every force encountered in mechanics does not have an associated potential energy. For example, work done by friction over a closed path is not zero and no potential energy can be associated with friction.
9. During a collision : (a) the total linear momentum is conserved at each instant of the collision ; (b) the kinetic energy conservation (even if the collision is elastic) applies after the collision is over and does not hold at every instant of the collision. In fact the two colliding objects are deformed and may be momentarily at rest with respect to each other.
6.1 The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) work done by gravitational force in the above case,
(c) work done by friction on a body sliding down an inclined plane,
(d) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,
(e) work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
6.2 A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the
(a) work done by the applied force in 10 s,
(b) work done by friction in 10 s,
(c) work done by the net force on the body in 10 s,
(d) change in kinetic energy of the body in 10 s,
and interpret your results.
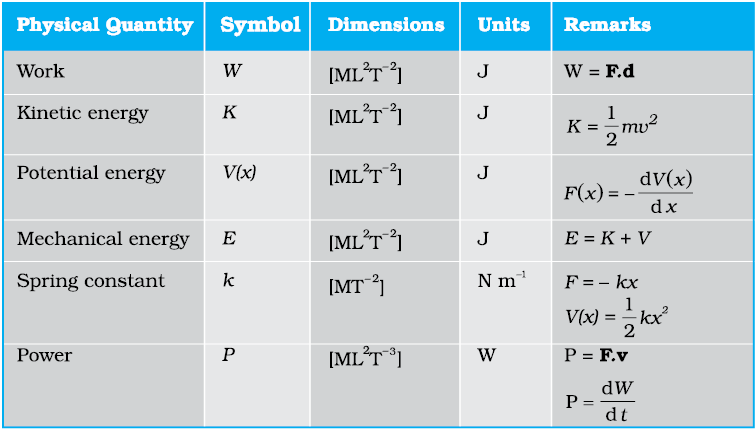
6.3 Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
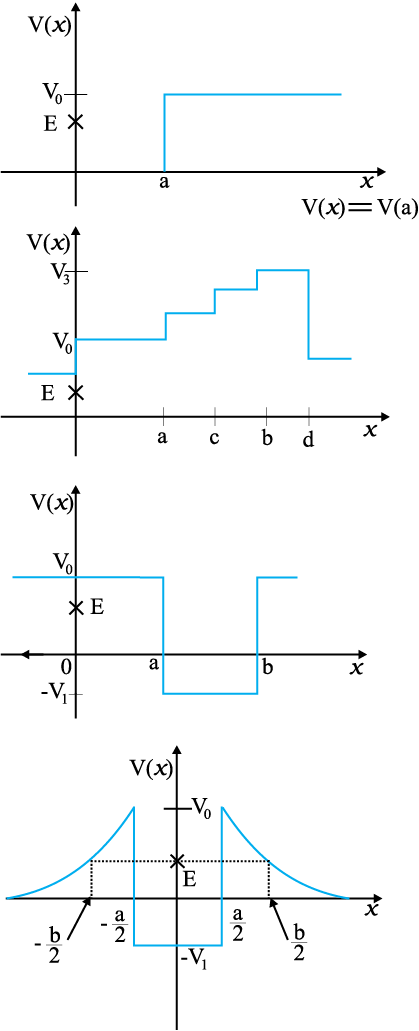
Fig. 6.11
6.4 The potential energy function for a particle executing linear simple harmonic motion is given by V(x) = kx2/2, where k is the force constant of the oscillator. For k = 0.5 N m-1, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.
6.5 Answer the following :
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ?
(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?
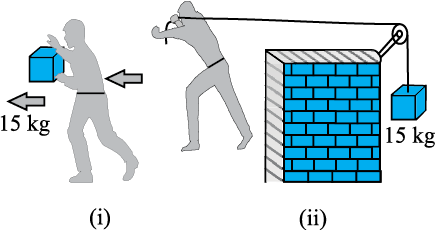
Fig. 6.13
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?
6.6 Underline the correct alternative :
(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.
(c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.
(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.
6.7 State if each of the following statements is true or false. Give reasons for your answer.
(a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.
(b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
(c) Work done in the motion of a body over a closed loop is zero for every force in nature.
(d) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
6.8 Answer carefully, with reasons :
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact) ?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls ?
(c) What are the answers to (a) and (b) for an inelastic collision ?
(d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic ? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
6.9 A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
(i) t1/2 (ii) t (iii) t3/2 (iv) t2
6.10 A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
(i) t1/2 (ii) t (iii) t3/2 (iv) t2
6.11 A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
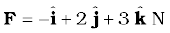
where  are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
6.12 An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton ? Obtain the ratio of their speeds. (electron mass = 9.11×10-31 kg, proton mass = 1.67×10–27 kg, 1 eV = 1.60 ×10–19 J).
6.13 A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey ? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10 m s–1 ?
6.14 A molecule in a gas container hits a horizontal wall with speed 200 m s–1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
6.15 A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump ?
6.16 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig. 6.14) is a possible result after collision ?
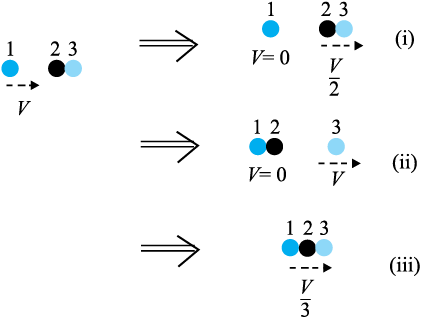
Fig. 6.14
6.17 The bob A of a pendulum released from 30o to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.
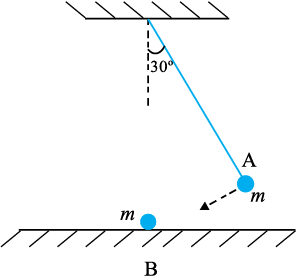
Fig. 6.15
6.18 The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance ?
6.19 A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg s–1. What is the speed of the trolley after the entire sand bag is empty ?
6.20 A body of mass 0.5 kg travels in a straight line with velocity v =a x3/2 where a = 5 m–1/2 s–1. What is the work done by the net force during its displacement from x = 0 to x = 2 m ?
6.21 The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t ? (b) What is the kinetic energy of the air ? (c) Assume that the windmill converts 25% of the wind’s energy into electrical energy, and that A = 30 m2, v = 36 km/h and the density of air is 1.2 kg m–3. What is the electrical power produced ?
6.22 A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. (a) How much work does she do against the gravitational force ? (b) Fat supplies 3.8 × 107J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?
6.23 A family uses 8 kW of power. (a) Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW? (b) Compare this area to that of the roof of a typical house.
6.1 The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) work done by gravitational force in the above case,
(c) work done by friction on a body sliding down an inclined plane,
(d) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,
(e) work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
6.2 A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the
(a) work done by the applied force in 10 s,
(b) work done by friction in 10 s,
(c) work done by the net force on the body in 10 s,
(d) change in kinetic energy of the body in 10 s,
and interpret your results.
6.3 Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

Fig. 6.11
6.4 The potential energy function for a particle executing linear simple harmonic motion is given by V(x) = kx2/2, where k is the force constant of the oscillator. For k = 0.5 N m-1, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

6.5 Answer the following :
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why ?
(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?

Fig. 6.13
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?
6.6 Underline the correct alternative :
(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.
(c) The rate of change of total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.
(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.
6.7 State if each of the following statements is true or false. Give reasons for your answer.
(a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.
(b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
(c) Work done in the motion of a body over a closed loop is zero for every force in nature.
(d) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
6.8 Answer carefully, with reasons :
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact) ?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls ?
(c) What are the answers to (a) and (b) for an inelastic collision ?
(d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic ? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
6.9 A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
(i) t1/2 (ii) t (iii) t3/2 (iv) t2
6.10 A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
(i) t1/2 (ii) t (iii) t3/2 (iv) t2
6.11 A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by
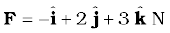
where  are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
6.12 An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton ? Obtain the ratio of their speeds. (electron mass = 9.11×10-31 kg, proton mass = 1.67×10–27 kg, 1 eV = 1.60 ×10–19 J).
6.13 A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey ? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10 m s–1 ?
6.14 A molecule in a gas container hits a horizontal wall with speed 200 m s–1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
6.15 A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump ?
6.16 Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig. 6.14) is a possible result after collision ?

Fig. 6.14
6.17 The bob A of a pendulum released from 30o to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

Fig. 6.15
6.18 The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance ?
6.19 A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg s–1. What is the speed of the trolley after the entire sand bag is empty ?
6.20 A body of mass 0.5 kg travels in a straight line with velocity v =a x3/2 where a = 5 m–1/2 s–1. What is the work done by the net force during its displacement from x = 0 to x = 2 m ?
6.21 The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t ? (b) What is the kinetic energy of the air ? (c) Assume that the windmill converts 25% of the wind’s energy into electrical energy, and that A = 30 m2, v = 36 km/h and the density of air is 1.2 kg m–3. What is the electrical power produced ?
6.22 A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. (a) How much work does she do against the gravitational force ? (b) Fat supplies 3.8 × 107J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?
6.23 A family uses 8 kW of power. (a) Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW? (b) Compare this area to that of the roof of a typical house.
6.24 A bullet of mass 0.012 kg and horizontal speed 70 m s–1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
6.25 Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given θ1 = 300, θ2 = 600, and h = 10 m, what are the speeds and times taken by the two stones ?
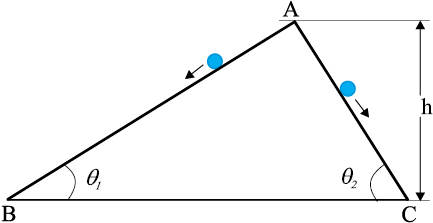
Fig. 6.16
6.26 A 1 kg block situated on a rough incline is connected to a spring of spring constant 100 N m–1 as shown in Fig. 6.17. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
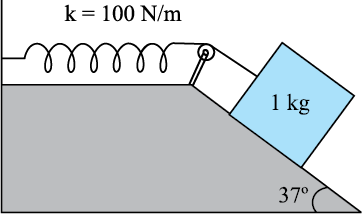
Fig. 6.17
6.27 A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with an uniform speed of 7 m s–1. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact ? Would your answer be different if the elevator were stationary ?
6.28 A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of 4 m s–1 relative to the trolley in a direction opposite to the its motion, and jumps out of the trolley. What is the final speed of the trolley ? How much has the trolley moved from the time the child begins to run ?
6.29 Which of the following potential energy curves in Fig. 6.18 cannot possibly describe the elastic collision of two billiard balls ? Here r is the distance between centres of the balls.
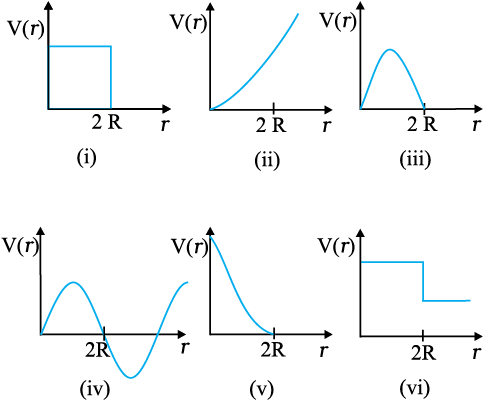
Fig. 6.18
6.30 Consider the decay of a free neutron at rest : n → gp + e–
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus (Fig. 6.19).
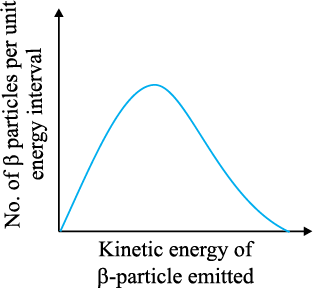
Fig. 6.19
[Note: The simple result of this exercise was one among the several arguments advanced by W. Pauli to predict the existence of a third particle in the decay products of β-decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin ½ (like e—, p or n), but is neutral, and either massless or having an extremely small mass (compared to the mass of electron) and which interacts very weakly with matter. The correct decay process of neutron is : n → g p + e– + ν ]
The table below lists the approximate power expended by an adult human of mass 60 kg.
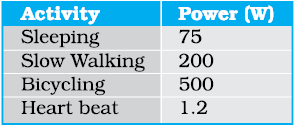
Mechanical work must not be confused with the everyday usage of the term work. A woman standing with a very heavy load on her head may get very tired. But no mechanical work is involved. That is not to say that mechanical work cannot be estimated in ordinary human activity.
Consider a person walking with constant speed v0. The mechanical work he does may be estimated simply with the help of the work-energy theorem. Assume :
(a) The major work done in walking is due to the acceleration and deceleration of the legs with each stride (See Fig. 6.20).
(b) Neglect air resistance.
(c) Neglect the small work done in lifting the legs against gravity.
(d) Neglect the swinging of hands etc. as is common in walking.
As we can see in Fig. 6.20, in each stride the leg is brought from rest to a speed, approximately equal to the speed of walking, and then brought to rest again.
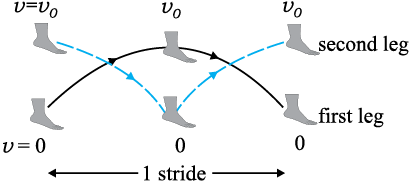
Fig. 6.20 An illustration of a single stride in walking. While the first leg is maximally off the round, the second leg is on the ground and vice-versa
The work done by one leg in each stride is by the work-energy theorem. Here ml is the mass of the leg. Note energy is expended by one set of leg muscles to bring the foot from rest to speed v0 while an additional is expended by a complementary set of leg muscles to bring the foot to rest from speed v0. Hence work done by both legs in one stride is (study Fig. 6.20 carefully)
Assuming mass of the leg ml = 10 kg and slow running with a speed of 10 km in a hour which translates to
approximately 3 m s-1, we obtain
If we take a stride to be 2 m long, the person covers 1.5 strides per second at his speed of 3 m s-1. Thus the power expended
= 270 W
We must bear in mind that this is a lower estimate since several avenues of power loss (e.g. swinging of hands, air resistance, etc.) have been ignored. The interesting point is that we did not worry about the forces involved. The forces, mainly friction and those exerted on the leg by the muscles of the rest of the body are hard to estimate. Static friction does no work and we bypassed the impossible task of estimating the work done by the muscles by taking recourse to the work-energy theorem. We can also see the advantage of a wheel. The wheel permits smooth locomotion without the continual starting and stopping in mammalian locomotion.
Exercises
Question 6.1:
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) work done by the gravitational force in the above case,
(c) work done by friction on a body sliding down an inclined plane,
(d) work is done by an applied force on a body moving on a rough horizontal plane with uniform velocity, (e) work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
NEETprep AnswerQuestion 6.2:
A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with a coefficient of kinetic friction = 0.1. Compute the
(a)work done by the applied force in 10 s, (b) work is done by friction in 10 s,
(c) work done by the net force on the body in 10 s,
(d) change in kinetic energy of the body in 10 s,
and interpret your results.
NEETprep AnswerQuestion 6.3:
Given in Fig. 6.11 are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.
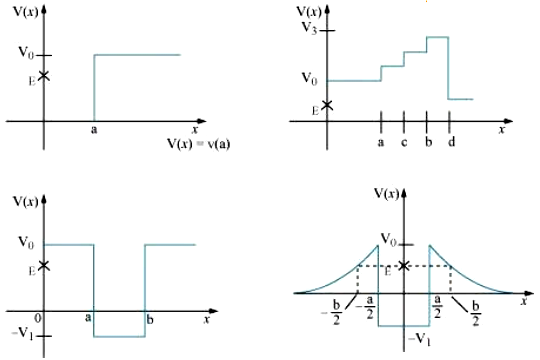
Question 6.4:
The potential energy function for a particle executing linear simple harmonic motion is given by V(x) =, where k is the force constant of the oscillator. For k = 0.5 N/m, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.
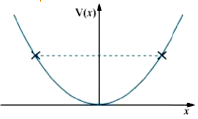
Question 6.5:
Answer the following:
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
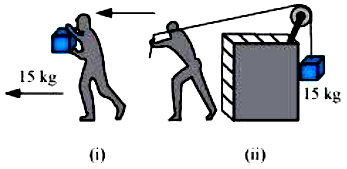
Question 6.6:
Underline the correct alternative:
(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/remains unaltered.
(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.
(c) The rate of change of the total momentum of a many-particle system is proportional to the external force/sum of the internal forces on the system.
(d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total energy of the system of two bodies.
Question 6.7:
State if each of the following statements is true or false. Give reasons for your answer.
(a) In an elastic collision of two bodies, the momentum, and energy of each body is conserved.
(b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.
(c) Work done in the motion of a body over a closed loop is zero for every force in nature.
(d) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.
Question 6.8:
Answer carefully, with reasons:
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls?
(c) What are the answers to (a) and (b) for an inelastic collision?
(d) If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during a collision, not gravitational potential energy).
Question 6.9:
A body is initially at rest. It undergoes a one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
Question 6.10:
A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time t is proportional to
Question 6.11:
A body constrained to move along the z-axis of a coordinate system is subject to a constant force given by
Where are unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis?
NEETprep AnswerQuestion 6.12:
An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds. (electron mass = , proton mass = , 1 eV = ).
NEETprep AnswerQuestion 6.13:
A raindrop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until, at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is ?
NEETprep AnswerQuestion 6.14:
A molecule in a gas container hits a horizontal wall with speed and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision? Is the collision elastic or inelastic?
NEETprep AnswerA pump on the ground floor of a building can pump up water to fill a tank of volume in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?
NEETprep Answer
Question 6.16:
Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following figure is a possible result after collision?
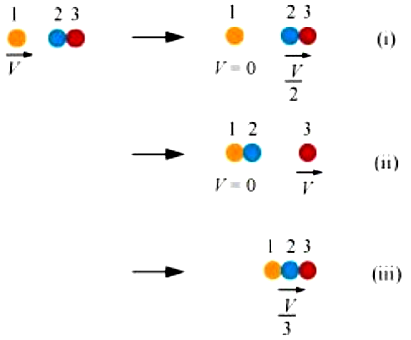
Question 6.17:
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. 6.15. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.
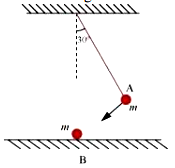
Question 6.18:
The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipated 5% of its initial energy against air resistance?
NEETprep AnswerQuestion 6.19:
A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, the sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg . What is the speed of the trolley after the entire sandbag is empty?
NEETprep AnswerQuestion 6.20:
A body of mass 0.5 kg travels in a straight line with velocity where . What is the work done by the net force during its displacement from x = 0 to x = 2 m?
NEETprep AnswerQuestion 6.21: The blades of a windmill sweep out a circle of area A. (a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t? (b) What is the kinetic energy of the air? (c) Assume that the windmill converts 25% of the wind’s energy into electrical energy and that A = 30 , v = 36 km/h and the density of air is 1.2 kg . What is the electrical power produced?
NEETprep AnswerQuestion 6.22:
A person trying to lose weight (dieter) lifts a 10 kg mass, one thousand times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated. (a) How much work does she do against the gravitational force? (b) Fat supplies 3.8 × 107 J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up?
NEETprep AnswerQuestion 6.23:
A family uses 8 kW of power. (a) Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW? (b) Compare this area to that of the roof of a typical house.
NEETprep AnswerQuestion 6.24:
A bullet of mass 0.012 kg and horizontal speed strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceiling by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
NEETprep AnswerQuestion 6.25:
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there at the same speed? Explain. , and h = 10 m, what are the speeds and times taken by the two stones?
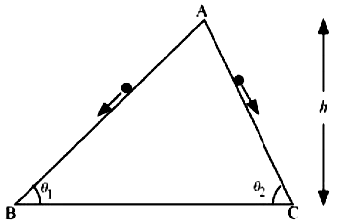
Question 6.26:
A 1 kg block situated on a rough incline is connected to a spring of spring constant as shown in Fig. 6.17. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.
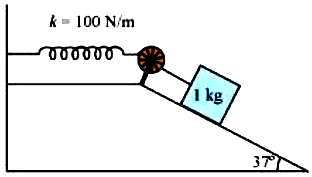
Question 6.27:
A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with a uniform speed of . It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact? Would your answer be different if the elevator were stationary?
NEETprep AnswerA trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg runs on the trolley from one end to the other (10 m away) with a speed of relative to the trolley in a direction opposite to its motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
NEETprep Answer
Question 6.29:
Which of the following potential energy curves in Fig. 6.18 cannot possibly describe the elastic collision of two billiard balls? Here r is the distance between centres of the balls.
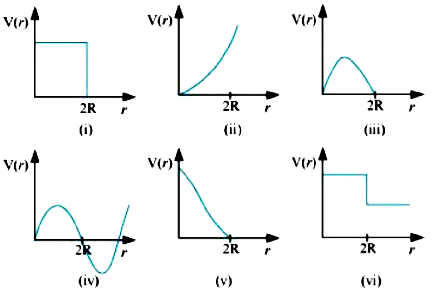
Question 6.30:
Consider the decay of a free neutron at rest: n → p+
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the β-decay of a neutron or a nucleus (Fig. 6.19).
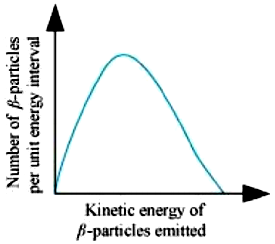
[Note: The simple result of this exercise was one among the several arguments advanced by W. Pauli to predict the existence of a third particle in the decay products of β-decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin ½ (like , p or n), but is neutral, and either massless or having an extremely small mass (compared to the mass of an electron) and which interacts very weakly with matter. The correct decay process of neutron is
NEETprep AnswerEXEMPLAR QUESTIONS
Q.1 An electron and a proton are moving under the influence of mutual forces. In calculating the change in the kinetic energy of the system during motion, one ignores the magnetic force of one on another. This is, because
(a) the two magnetic forces are equal and opposite, so they produce no net effect
(b) the magnetic forces do not work on each particle
(c) the magnetic forces do equal and opposite (but non-zero) work on each panicle
(d) the magnetic forces are necessarily negligible
Q.2 A proton is kept at rest. A positively charged particle is released from rest at a distance d in its field. Consider two experiments; one in which the charged particle is also a proton and in another, a positron. At the same time t, the work done on the two moving charged particles is
(a) same as the same force law is involved in the two experiments
(b) less for the case of a position, as the position moves away more rapidly and the force on it weakens
(c) more for the case of a position, as the position moves away from a larger distance
(d) same as the work done by cha particle on the stationary proton
Q. 3 A man squatting on the ground gets straight up and stand. The force of reaction of ground on the man during the process is
(a) constant and equal to mg in magnitude
(b) constant and greater than mg in magnitude
(c) variable but always greater than mg
(d) at first, greater than mg and later becomes equal to mg
Q. 4 A bicyclist comes to a skidding stop in 10 m. During this process, the force on the bicycle due to the road is 200N is directly opposed to the motion. The work done by the cycle on the road is
(a) + 2000J
(b) - 200J
(c) zero
(d) -20,000J
Q. 5 A body is falling freely under the action of gravity alone in a vacuum.
Which of the following quantities remain constant during the fall?
(a) Kinetic energy (b) Potential energy
(c) Total mechanical energy (d) Total linear momentum
Q. 6 During inelastic collision between two bodies, which of the following
quantities always remain conserved?
(a) Total kinetic energy (b) Total mechanical energy
(c) Total linear momentum (d) Speed of each body
Q. 7 Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track as shown in the figure.
Which of the following statement is correct?
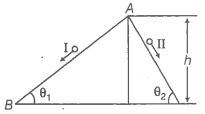
(a) Both the stones reach the bottom at the same time but not at the same speed
(b) Both the stones reach the bottom with the same speed and stone reaches the bottom earlier than stone
(c) Both the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I
(d) Both the stones reach the bottom at different times and at different speeds
Q.8 The potential energy function for a particle executing linear SHM is given by where k is the force constant of the oscillator (Fig). For k = 0.5 N/m, the graph ofV(x) versus x is shown in the figure. A particle of total energy E turns back when it reaches . If V and K indicate the PE and KE, respectively of the particle at , then which of the following is correct?
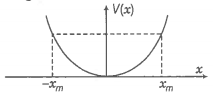
Q. 9 Two identical ball bearings in contact with each other and resting on a frictionless table is hit head-on by another ball bearing of the same time a moving initially with a speed v as shown in the figure.
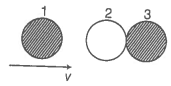
If the collision is elastic, which of the following (figure) is a possible result after collision?
Q. 10 A body of mass 0.5 kg travels in a straight line with velocity / where . The work is done by the net force during its displacement from x = O to x = 2 m is
(a) 15 J (b) 50 J
(c) 10 J (d) 100 J
EXEMPLAR QUESTIONS
Q.11 A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in the figure correctly shown the displacement-time curve for its motion?
Q.12 Which of the diagrams shown in the figure most closely shows the variation in kinetic energy of the earth as it moves once around the sun in its elliptical orbit?
Q. 13 Which of the diagrams shown in the figure represents the variation of to mechanical energy of a pendulum oscillating in the air as a function of time.
Q. 14 A mass of 5 kg is moving along a circular path of radius 1 m. If the mas moves with 300 rev/min, its kinetic energy would be
(a) 250
(b) 100
(c) 5
(d) 0
NEETprep Answer
Q.15 A raindrop falling from a height h above ground, attains a near-terminal velocity when it has fallen through a height (3/4)h. Which of the diagrams shown in figure correctly shows the change in kinetic and potential energy of the drop during its fall up to the ground?
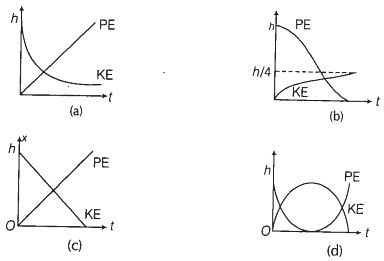
Q.16 In a shotput event an athlete throws the shotput of mass 10 kg with an initial speed of 1 m/s at 450 from a height 1.5 m above ground. Assuming air resistance to be negligible and acceleration due to gravity to be 10 m/, the kinetic energy of the shotput when it just reaches the ground will be
(a) 2.5 J
(b) 5.0 J
(c) 52.5 J
(d) 155.0 J
NEETprep Answer
Q. 17 Which of the diagrams in the figure correctly shows the change in kinetic energy of an iron sphere falling freely in a lake having sufficient density to impart it a terminal velocity?
Q. 18 A cricket ball of mass 150 g moving with a speed of 126 km/h hits at the middle of the bat, held firmly at its position by the batsman. The ball moves straight back to the bowler after hitting the bat. Assuming that collision between ball and bat is completely elastic and the two remains in contact for 0.001s, the force that the batsman had to apply to hold the bat firmly at its place would be
(a) 10.5 N (b) 21 N (c) 105 X N (d) 2.1 x N
NEETprep Answer
Q. 19 A man of mass m, standing at the bottom of the staircase, of height L, climbs it and stands at its top.
(a) Work done by all forces on man is equal to the rise in energy mgL
(b) Work done by all forces on man is zero
(c) Work done by the gravitational force on man is mgL
(d) The reaction force from a step does not do work the point of the application of the force does not move while the force exists
Q. 20 A bullet of mass m fired at 300 to the horizontal leaves the barrel of the gun with a velocity v. The bullet hits a soft target at a height h above the ground while it is moving downward and emerge out with half the kinetic energy it had before hitting the target.
Which of the following statements are correct in respect of the bullet after it emerges out of the target?
(a) The velocity of the bullet will be reduced to half its initial value
(b) The velocity of the bullet will be more than half of its earlier velocity
(c) The bullet will continue to move along the same parabolic path
(d) The bullet will move in a different parabolic path
(e) The bullet will fall vertically downward after hitting the target
(f) The internal energy of the particles of the target will increase
EXEMPLAR QUESTIONS
Q. 21 Two blocks and having equal mass are free to move on a horizontal frictionless surface. is attached to a massless spring as shown in the figure. Initially is at rest and is moving toward with speed v and collides head-on with .
(a) While spring is fully compressed all the KE of is as PE of spring
(b) While spring is fully compressed the system momentum is not conserved, though final momentum is equal to the initial momentum
(c) If spring is massless, the final state of the is the state of rest
(d) If the surface on which blocks are moving has friction, then a collision cannot be
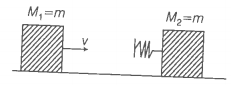
Q.22 A rough inclined plane is placed on a cart moving with a constant velocity u on horizontal ground. A block of mass M rests on the incline. Is any work done by a force of friction between the block and incline? Is there then a dissipation of energy?
Q.23 Why is electrical power required at all when the elevator is descending? Why should there be a limit on the number of passengers in this case?
Q. 24 A body is being raised to a height h from the surface of the earth. What is the sign of work done by
(a) applied force and
(b) gravitational force?
Q.25 Calculate the work done by a car against gravity in moving along a straight horizontal road. The mass of the car is 400 kg and the distance. moved is 2 m.
Q. 26 A body falls towards earth in the air. Will its total mechanical energy be conserved during the fall? Justify'.
Q. 27 A body is moved along a closed loop. Is the work done in moving the body necessarily zero? If not, state the condition under which work done over a closed path is always zero.
Q.28 In an elastic collision of two billiard balls, which of the following quantities remain conserved during the short time of collision of the balls (i.e., when they are in contact)?
(a) Kinetic energy.
(b) Total linear momentum.
Give the reason for your answer in each case.
Q.29 Calculate the power of a crane in watts, which lifts a mass of 100 kg to a
height of 10 m in the 20s.
Q.30 The average work done by a human heart while it beats once is 0.5 J. Calculate the power used by the heart if it beats 72 times in a minute.
EXEMPLAR QUESTIONS
Q.31 Give an example of a situation in which an applied force does not result in a change in kinetic energy.
NEETprep Answer
Q.32 Two bodies of unequal mass are moving in the same direction with equal kinetic energy. The two bodies are brought to rest by applying retarding force of the same magnitude. How would the distance moved by them before coming to rest compare?
NEETprep Answer
Q. 33 A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in the figure.
What will be the trajectory of the particle, if the string is cut at
(a) point B?
(b) point C?
(c) point X?
Q.34 A graph of potential energy V (x) versus xis shown in the figure. A particle of energy is executing motion in it. Draw graph of velocity and kinetic energy versus x for one complete cycle AFA.

Q.35 A ball of mass m, moving with a speed , collide inelastically (e > 0) with an identical ball at rest. Show that
(a) For head-on collision, both the balls move forward.
(b) For a general collision, the angle between the two velocities of scattered balls is less than 90.
Q.36 Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C, and D in which the relation between potential energy V, kinetic energy (K), and total energy E is as given below
Region A : V > E Region B : V < E
Region C : K < E Region D : V > E
State with reason in each case whether a particle can be found in the given region or not.
NEETprep Answer
Q.37 The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in the figure.
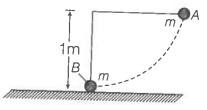
If the length of the pendulum is 1m, calculate
(a) the height to which bob A will rise after the collision.
(b) the speed with which bob B starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
When ball A reaches the bottom point its velocity is horizontal henæ, we can apply conservation of linear momentum in the horizontal direction.
NEETprep Answer
Q.38 A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 m/s. Calculate
(a) the loss of PE of the drop.
(b) the gain in KE of the drop.
(c) Is the gain in KE equal to the loss of PE? If not why? Take, g 10 m/
Q.39 Two pendulums with identical bobs and lengths are suspended from common support such that in rest position the two bobs are in contact (figure). One of the bobs is released after being displaced by 100 so that it collides elastically head-on with the other bob.
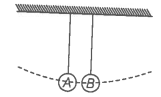
(a) Describe the motion of two bobs.
(b) Draw a graph showing variation in energy of either pendulum with time, for . where T is the period of each pendulum.
NEETprep Answer
Q.40 Suppose the average mass of raindrops is 3.0 x kg and their average terminal velocity 9 m/s. Calculate the energy transferred by rain to each square metre of the surface at a place that receives 100cm of rain in a year.
NEETprep AnswerEXEMPLAR QUESTIONS
Q. 41 An engine is attached to a wagon through a shock absorber of length 1.5 m. The system with a total mass of 50,000 kg is moving with a speed of 36 km/h when the brakes are applied to bring it to rest. In the process of the system being brought to rest, the spring of the shock absorber gets compressed by 1.0 m. If 90% of the energy of the wagon is lost due to friction, calculate the spring constant.
Q.42. An adult weighing 600 N raises the center of gravity of his body by 0.25m While taking each step of 1 m length in jogging. If he jogs for 6 km, calculate the energy utilized by him in jogging assuming that there is no energy loss due to friction of ground and air. Assuming that the body of the adult is capable of converting energy intake in the form of food, calculate the energy equivalents of food that would be required to compensate energy utilized for jogging.
NEETprep AnswerQ43. On complete combustion, a liter of petrol gives off heat equivalent to 3 x 107 J. In a test drive, a car weighing 1200 kg including the mass of the driver, runs 15 km per liter while moving with a uniform speed on a straight track. Assuming that friction offered by the road surface and air to be uniform, calculate the force of friction acting on the car during the test drive if the efficiency of the car engine were 0.5.
NEETprep AnswerQ.44 A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30 by a force of 10 N parallel to the inclined surface (figure). The coefficient of friction between the block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate
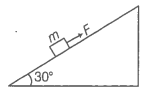
(a) work done against gravity
(b) work done against force of friction
(c) increases in potential energy
(d) increase in kinetic energy
(e) work done by applied force
Q.45 A curved surface is shown in the figure. The portion BCD is free of friction. There are three spherical balls of identical radii and masses. Balls are released from rest one by one from A which is at a slightly greater height than C.
With the surface AB, ball 1 has large enough friction to cause rolling down without slipping; ball 2 has small friction and ball 3 has negligible friction.
(a) For which balls are total mechanical energy conserved?
(b) Which ball (s) can reach D?
(c) For balls that do not reach D, which of the balls can reach back A?
Q.46 A rocket accelerates straight up by ejecting gas downwards. In a small time interval t, it ejects a gas of mass Am at a relative speed u. Calculate KE of the entire system at t + t and t and show that the device that ejects gas does work = (1/2) in this time interval (negative gravity).
Q.47 Two identical steel cubes (masses 50g, side 1 cm) collide head-on face to face with a space of 10 cm/s each. Find the maximum compression of each. Young's modulus for steel .
Q.48 A balloon filled with helium rises against gravity increasing its potential energy. The speed of the balloon also increases as it rises. How do you reconcile this with the law of conservation of mechanical energy? You can neglect the viscous drag of air and assume that the density of air is constant.
