Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 x 10-22 C/m2. The electric field between the plates is:
1. 0.96 × 10-10 N/C
2. 1.92 × 10- 10 N/C
3. 0
4. 3.84 × 10-10 N/C
1. 0.96 × 10-10 N/C
2. 1.92 × 10- 10 N/C
3. 0
4. 3.84 × 10-10 N/C
An oil drop of \(12\) excess electrons is held stationary under a constant electric field of \(2.55\times10^{4}\text{ N/C}.\) The density of the oil is \(1.26\text{ g/cm}^3.\) The radius of the drop is:
1. \(9.82\times10^{-4}\text{ mm}\)
2. \(9.82\times10^{-7}\text{ mm}\)
3. \(8.92\times10^{-4}\text{ mm}\)
4. \(8.92\times10^{-7}\text{ mm}\)
Which among the curves shown in the figure represents electrostatic field lines?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | \(10^{-2}~\text{N-m}\) |
2. | \(0\) |
| 3. | \(10^{-1}~\text{N-m}\) |
4. | \(0.01~\text{N-m}\) |
A hollow charged conductor has a tiny hole cut into its surface. The electric field in the hole is:
1. \(\left(\frac{3 \sigma}{\varepsilon_0}\right) \widehat{n}\)
2. \(\left(\frac{2 \sigma}{\varepsilon_0}\right) \widehat{n}\)
3. \(\left(\frac{\sigma}{2 \varepsilon_0}\right) \widehat{n}\)
4. \(\left(\frac{\sigma}{\varepsilon_0}\right) \widehat{n}\)
A particle of mass m and charge (–q) enters the region between the two charged plates initially moving along the x-axis with speed (as shown in the figure). The length of the plate is L and a uniform electric field E is maintained between the plates. The vertical deflection of the particle at the far edge of the plate is:
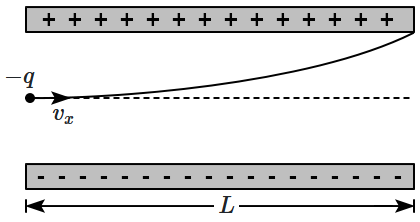
1. \(\frac{2 q E L^2}{3 m\left(v_x\right)^2}\)
2. \(\frac{2 q E L^2}{m\left(v_x\right)^2}\)
3. \(\frac{3 q E L^2}{2 m\left(v_x\right)^2}\)
4. \(\frac{q E L^2}{2 m\left(v_x\right)^2}\)
| 1. | \(\dfrac{Q+q}{4 \pi r_{2}^{2}}\) | 2. | \(\dfrac{q}{4 \pi r_{1}^{2}}\) |
| 3. | \(\dfrac{-Q+q}{4 \pi r_{2}^{2}}\) | 4. | \(\dfrac{-q}{4 \pi r_{1}^{2}}\) |
A long charged cylinder of linear charged density is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders at distance d from the common axis?
1. \(\frac{2 \lambda}{\pi \varepsilon_0 d}\)
2. \(\frac{\lambda}{2 \pi \varepsilon_0 d}\)
3. \(\frac{\lambda}{\pi \varepsilon_0 d}\)
4. \(\frac{\pi \lambda}{2 \varepsilon_0 d}\)
Sure check for the presence of electric charge is:
1. Process of induction
2. Repulsion between bodies
3. Attraction between bodies
4. Frictional force between bodies
If a solid and a hollow conducting sphere have the same radii then:
1. the hollow sphere will hold more maximum charge.
2. the solid sphere will hold more maximum charge.
3. both the spheres will hold the same maximum charge.
4. both the spheres can't hold a charge.






