A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of . The charge on the sphere is:
1. 2 .077 × 10-3 C
2. 2. 453 × 10-3C
3. 1. 447 × 10-3C
4. 3. 461 × 10-3C
1. 2 .077 × 10-3 C
2. 2. 453 × 10-3C
3. 1. 447 × 10-3C
4. 3. 461 × 10-3C
An infinite line charge produces a field of \(9\times10^{4}~\text{N/C}\) at a distance of \(2~\text{cm}\). The linear charge density is:
1. \(0.1~\mu\text{C/m}\)
2. \(100~\mu\text{C/m}\)
3. \(1.0~\mu\text{C/m}\)
4. \(10~\mu\text{C/m}\)
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 x 10-22 C/m2. The electric field between the plates is:
1. 0.96 × 10-10 N/C
2. 1.92 × 10- 10 N/C
3. 0
4. 3.84 × 10-10 N/C
An oil drop of 12 excess electrons is held stationary under a constant electric field of . The density of the oil is . The radius of the drop is:
1. \(9.82\times10^{-4}\) mm
2. \(9.82\times10^{-7}\) mm
3. \(8.92\times10^{-4}\) mm
4. \(8.92\times10^{-7}\) mm
Which among the curves shown in the figure represents electrostatic field lines?
| 1. |  |
2. |  |
| 3. |  |
4. |  |
| 1. | \(10^{-2}~\text{N-m}\) |
2. | \(0\) |
| 3. | \(10^{-1}~\text{N-m}\) |
4. | \(0.01~\text{N-m}\) |
A hollow charged conductor has a tiny hole cut into its surface. The electric field in the hole is:
1. \(\left(\frac{3 \sigma}{\varepsilon_0}\right) \widehat{n}\)
2. \(\left(\frac{2 \sigma}{\varepsilon_0}\right) \widehat{n}\)
3. \(\left(\frac{\sigma}{2 \varepsilon_0}\right) \widehat{n}\)
4. \(\left(\frac{\sigma}{\varepsilon_0}\right) \widehat{n}\)
A particle of mass m and charge (–q) enters the region between the two charged plates initially moving along the x-axis with speed (as shown in the figure). The length of the plate is L and a uniform electric field E is maintained between the plates. The vertical deflection of the particle at the far edge of the plate is:
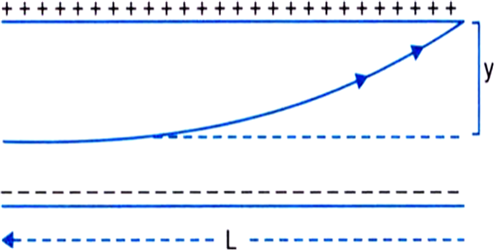
1. \(\frac{2 q E L^2}{3 m\left(v_x\right)^2}\)
2. \(\frac{2 q E L^2}{m\left(v_x\right)^2}\)
3. \(\frac{3 q E L^2}{2 m\left(v_x\right)^2}\)
4. \(\frac{q E L^2}{2 m\left(v_x\right)^2}\)
| 1. | \(\dfrac{Q+q}{4 \pi r_{2}^{2}}\) | 2. | \(\dfrac{q}{4 \pi r_{1}^{2}}\) |
| 3. | \(\dfrac{-Q+q}{4 \pi r_{2}^{2}}\) | 4. | \(\dfrac{-q}{4 \pi r_{1}^{2}}\) |
A long charged cylinder of linear charged density is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders at distance d from the common axis?
1. \(\frac{2 \lambda}{\pi \varepsilon_0 d}\)
2. \(\frac{\lambda}{2 \pi \varepsilon_0 d}\)
3. \(\frac{\lambda}{\pi \varepsilon_0 d}\)
4. \(\frac{\pi \lambda}{2 \varepsilon_0 d}\)




