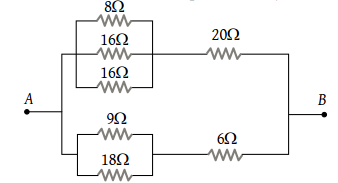
Equivalent resistance between A and B will be

1. 2 ohm
2. 18 ohm
3. 6 ohm
4. 3.6 ohm

Referring to the figure below, the effective resistance of the network is
1. 2r
2. 4r
3. 10r
4. 5r/2
Two resistances are joined in parallel whose resultant is ohm. One of the resistance wire is broken and the effective resistance becomes 2Ω. Then the resistance in ohm of the wire that got broken was
1. 3/5
2. 2
3. 6/5
4. 3
The equivalent resistance of resistors connected in series is always :
1. Equal to the mean of component resistors
2. Less than the lowest of component resistors
3. In between the lowest and the highest of component resistors
4. Equal to the sum of component resistors
A cell of negligible resistance and e.m.f. 2 volts is connected to a series combination of 2, 3, and 5 . The potential difference in volts between the terminals of 3 resistance will be :
1. 0.6 V
2. 2/3 V
3. 3 V
4. 6 V
Four wires of equal length and of resistances 10 ohms each are connected in the form of a square. The equivalent resistance between two opposite corners of the square is :
1. 10 ohm
2. 40 ohm
3. 20 ohm
4. 10/4 ohm
Two resistors are connected (a) in series (b) in parallel. The equivalent resistance in the two cases is 9 ohm and 2 ohms respectively. Then the resistances of the component resistors are :
1. 2 ohm and 7 ohm
2. 3 ohm and 6 ohm
3. 3 ohm and 9 ohm
4. 5 ohm and 4 ohm
Resistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5-volt cell of negligible internal resistance is connected across a 3-ohm resistor, the current flowing through this resistance will be :
1. 0.25 amp
2. 0.5 amp
3. 1.0 amp
4. 1.5 amp
Resistances of 6 ohm each are connected in the manner shown in adjoining figure. With the current 0.5 ampere as shown in figure, the potential difference is
1. 3.6 V
2. 6.0 V
3. 3.0 V
4. 7.2 V
The equivalent resistance of the arrangement of resistances shown in adjoining figure between the points A and B is
1. 6 ohm
2. 8 ohm
3. 16 ohm
4. 24 ohm