Q. No.Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass.
1. \(2(\hat{i}+\hat{j})\)
2. \(\hat{i}+\hat{j}\)
3. \(\frac{2}{3}(\hat{i}+\hat{j})\)
4. \(\frac{4}{3}(\hat{i}+\hat{j})\)
1. \(2(\hat{i}+\hat{j})\)
2. \(\hat{i}+\hat{j}\)
3. \(\frac{2}{3}(\hat{i}+\hat{j})\)
4. \(\frac{4}{3}(\hat{i}+\hat{j})\)
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
1. \(C\)
2. \(D\)
3. \(A\)
4. \(B\)
A circular platform is mounted on a frictionless vertical axle. Its radius \(R = 2~\text{m}\) and its moment of inertia about the axle is \(200~\text{kg m}^2\). It is initially at rest. A \(50~\text{kg}\) man stands on the edge of the platform and begins to walk along the edge at the speed of \(1~\text{ms}^{-1}\) relative to the ground. The time taken by man to complete one revolution is:
| 1. | \(\dfrac{3\pi}{2}\text{s}\) | 2. | \(2\pi~\text{s}\) |
| 3. | \(\dfrac{\pi}{2}\text{s}\) | 4. | \(\pi~\text{s}\) |
Three masses are placed on the \(x\)-axis: \(300~\text{g}\) at origin, \(500~\text{g}\) at \(x= 40~\text{cm}\) and \(400~\text{g}\) at \(x= 70~\text{cm}.\) The distance of the centre of mass from the origin is:
1. \(45~\text{cm}\)
2. \(50~\text{cm}\)
3. \(30~\text{cm}\)
4. \(40~\text{cm}\)
From a circular disc of radius \(R\) and mass \(9M,\) a small disc of mass \(M\) and radius \(R/3\) is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is:
1. \(MR^{2}\)
2. \(4MR^{2}\)
3. \(\frac{4}{9}MR^{2}\)
4. \(\frac{40}{9}MR^{2}\)
The angular speed of the wheel of a vehicle is increased from \(360~\text{rpm}\) to \(1200~\text{rpm}\) in \(14\) seconds. Its angular acceleration will be:
1. \(2\pi ~\text{rad/s}^2\)
2. \(28\pi ~\text{rad/s}^2\)
3. \(120\pi ~\text{rad/s}^2\)
4. \(1 ~\text{rad/s}^2\)
From a circular ring of mass \({M}\) and radius \(R,\) an arc corresponding to a \(90^\circ\) sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is \(K\) times \(MR^2.\) The value of \(K\) will be:
| 1. | \(\frac{1}{4}\) | 2. | \(\frac{1}{8}\) |
| 3. | \(\frac{3}{4}\) | 4. | \(\frac{7}{8}\) |
A uniform rod of length \(200~ \text{cm}\) and mass \(500~ \text g\) is balanced on a wedge placed at \(40~ \text{cm}\) mark. A mass of \(2~\text{kg}\) is suspended from the rod at \(20~ \text{cm}\) and another unknown mass \(m\) is suspended from the rod at \(160~\text{cm}\) mark as shown in the figure. What would be the value of \(m\) such that the rod is in equilibrium?
(Take \(g=10~( \text {m/s}^2)\)
| 1. | \({\dfrac 1 6}~\text{kg}\) | 2. | \({\dfrac 1 {12}}~ \text{kg}\) |
| 3. | \({\dfrac 1 2}~ \text{kg}\) | 4. | \({\dfrac 1 3}~ \text{kg}\) |
Three identical spheres, each of mass \(M\), are placed at the corners of a right-angle triangle with mutually perpendicular sides equal to \(2~\text{m}\) (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, find the position vector of the centre of mass.
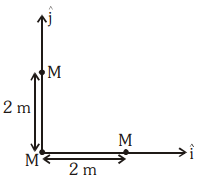
| 1. | \(2( \hat{i}+ \hat{j})\) | 2. | \(( \hat{i}+ \hat{j})\) |
| 3. | \({2 \over 3}( \hat{i}+ \hat{j})\) | 4. | \({4 \over 3}( \hat{i}+ \hat{j})\) |
Consider a system of two identical particles. One of the particles is at rest and the other has an acceleration \(\vec{a}\). The centre of mass has an acceleration:
| 1. | zero | 2. | \(\vec{a}/2\) |
| 3. | \(\vec{a}\) | 4. | \(2\vec{a}\) |
© 2025 GoodEd Technologies Pvt. Ltd.