For any arbitrary motion in space, which of the following relations is true?

1.	\(\vec{v}_{\text {avg }}=\frac{1}{2}\left[\vec{v}\left(t_1\right)+\vec{v}\left(t_2\right)\right]\)
2.	\(\vec{v}(t)=\vec{v}(0)+\vec{a} t\)
3.	\(\vec{r}({t})=\vec{r}(0)+\vec{v}(0){t}+\frac{1}{2} \vec{a}{t}^2\)
4.	\(\vec{v}_{\text {avg }}=\frac{\left[\vec{r}\left(t_2\right)-\vec{r}\left(t_1\right)\right]}{\left(t_2-t_1\right)}\)

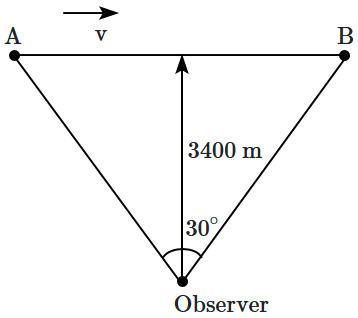
An aircraft is flying with speed \(v\) at a height of \(3400~\text{m}\) above the ground (As shown in the figure). If the angle subtended at a ground observation point by the aircraft positions \(10.0~\text{s}\) apart is \(30^{\circ}\), what is the speed of the aircraft? ( Take \(\tan15^{\circ} = 0.267\))
      

1. \(182~\text{m/s}\)
2. \(130~\text{m/s}\)
3. \(192~\text{m/s}\)
4. \(179~\text{m/s}\)

A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to be fixed, and neglect air resistance.

1. Yes
2. No
3. Depends on the mass of the bullet
4. None of the above

A fighter plane flying horizontally at an altitude of \(1.5~\text{km}\) with a speed of \(720~\text{km/hr}\) passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed $\mathrm{}$\(600~\text{m/s}\) to hit the plane?

A cyclist is riding at a speed of 27 km/h. As he approaches a circular turn on the road of a radius of 80 m, he applies brakes and reduces his speed at a constant rate of 0.50 m/s every second. What is the magnitude of the initial acceleration of the cyclist on the circular turn?

1. 0.66 ${\mathrm{ms}}^{-2}$

2. 0.56 ${\mathrm{ms}}^{-2}$

3. 0.86 ${\mathrm{ms}}^{-2}$

4. 0.16 ${\mathrm{ms}}^{-2}$

For a projectile, the angle between the velocity and the x-axis as a function of time is given by:

$\left(1\right)<mspace\; width="1em"></mspace>\mathrm{\theta }\left(\mathrm{t}\right)={\cos }^{-1}\left(\frac{{\mathrm{u}}_{\mathrm{y}}-\mathrm{gt}}{{\mathrm{u}}_{\mathrm{x}}}\right)$

$\left(2\right)<mspace\; width="1em"></mspace>\mathrm{\theta }\left(\mathrm{t}\right)={\sin }^{-1}\left(\frac{{\mathrm{u}}_{\mathrm{y}}-\mathrm{gt}}{{\mathrm{u}}_{\mathrm{x}}}\right)$

$\left(3\right)<mspace\; width="1em"></mspace>\mathrm{\theta }\left(\mathrm{t}\right)={\cot }^{-1}\left(\frac{{\mathrm{u}}_{\mathrm{y}}-\mathrm{gt}}{{\mathrm{u}}_{\mathrm{x}}}\right)$

$\left(4\right)<mspace\; width="1em"></mspace>\mathrm{\theta }\left(\mathrm{t}\right)={\tan }^{-1}\left(\frac{{\mathrm{u}}_{\mathrm{y}}-\mathrm{gt}}{{\mathrm{u}}_{\mathrm{x}}}\right)$

A truck starts from rest and accelerates uniformly at \(2.0~\text{ms}^{-2}\). At \(t = 10~\text{s}\), a stone is dropped by a person standing on the top of the truck (\(6\) m high from the ground). What is the acceleration of the stone at \(t = 11~\text{s}\)? (Neglect air resistance.)
1. \(10\) ms^–2 (upward)
2. \(15\) ms^–2 (downward)
3. \(10\) ms^–2 (downward)
4. \(15\) ms^–2 (upward)

A particle is moving along a circle such that it completes one revolution in \(40\) seconds. In \(2\) minutes \(20\) seconds, the ratio of \(|displacement| \over distance\) will be:
1. \(0\)
2. \(\dfrac{1}{7}\)
3. \(\dfrac{2}{7}\)
4. \(\dfrac{1}{11}\)

Consider the motion of the tip of the second hand of a clock. In one minute (assuming \(R\) to be the length of the second hand), its:

A car moves with a speed of \(60\) km/h for \(1\) hour in the east direction and with the same speed for \(30\) min in the south direction. The displacement of the car from the initial position is: