Coordinates of a particle as a function of time \(t\) are \(x= 2t\),
\(y =4t\). It can be inferred that the path of the particle will be:

1.	Straight line	2.	Ellipse
3.	Parabola	4.	Hyperbola

At an instant, the velocity and acceleration of a particle moving in the XY plane are $2\hat{\mathrm{i}} + 3\hat{\mathrm{j}}$ m/s and $-3\hat{\mathrm{i}}+2\hat{\mathrm{j}}$ $\mathrm{m}/{\mathrm{s}}^2$. Rate of change of speed of the particle at this instant is:

(1) $\sqrt{13}$ $\mathrm{m}/{\mathrm{s}}^2$

(2) -1 $\mathrm{m}/{\mathrm{s}}^2$

(3) 1 $\mathrm{m}/{\mathrm{s}}^2$

(4) Zero

A body started moving with an initial velocity of \(4\) m/s along the east and an acceleration \(1\) m/s² along the north. The velocity of the body just after \(4\) s will be?

A projectile thrown from the ground has horizontal range R. If velocity at the highest point is doubled somehow, the new range will be:

(1) 3 R

(2) 1.5 R

(3) $\sqrt{3}$ R

(4) 2 R

A particle is projected from the origin with velocity $\left(4\hat{\mathrm{i}} + 9\hat{\mathrm{j}}\right)$ m/s. The acceleration in the region is constant and -10$\hat{\mathrm{j}}$ $\mathrm{m}/{\mathrm{s}}^2$. The magnitude of velocity after one second is

(1) 8 m/s

(2) $\sqrt{15}$ m/s

(3) $\sqrt{17}$ m/s

(4) $\sqrt{27}$ m/s

A particle is moving on a circular path of radius \(R.\) When the particle moves from point \(A\) to \(B\) (angle \( \theta\)), the ratio of the distance to that of the magnitude of the displacement will be:

         
1. \(\dfrac{\theta}{\sin\frac{\theta}{2}}\)
2. \(\dfrac{\theta}{2\sin\frac{\theta}{2}}\)
3. \(\dfrac{\theta}{2\cos\frac{\theta}{2}}\)
4. \(\dfrac{\theta}{\cos\frac{\theta}{2}}\)

The horizontal range of a particle thrown from the ground is four times the maximum height. The angle of projection with the vertical is:

(1) 60°

(2) 30°

(3) 45°

(4) 90°

A particle is thrown with a velocity of 40 m/s. If it passes A and B as shown in the figure at time ${\mathrm{t}}_1$ = 1 s and ${\mathrm{t}}_2$ = 3 s. The value of h is:

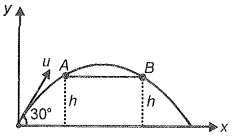
(1) 15 m

(2) 10 m

(3) 30 m

(4) 20 m

To a stationary man, the rain is falling on his back with a velocity v at an angle $\mathrm{\theta }$ with vertical. To make the rain-velocity perpendicular to the man, he:

(1) must move forward with a velocity vsin$\mathrm{\theta }$.

(2) must move forward with a velocity vtan$\mathrm{\theta }$.

(3) must move forward with a velocity vcos$\mathrm{\theta }$.

(4) should move in the backward direction.