The horizontal range of a particle thrown from the ground is four times the maximum height. The angle of projection with the vertical is:
(1) 60°
(2) 30°
(3) 45°
(4) 90°
A particle is thrown with a velocity of 40 m/s. If it passes A and B as shown in the figure at time = 1 s and = 3 s. The value of h is:
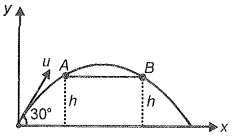
(1) 15 m
(2) 10 m
(3) 30 m
(4) 20 m
To a stationary man, the rain is falling on his back with a velocity v at an angle with vertical. To make the rain-velocity perpendicular to the man, he:
(1) must move forward with a velocity vsin.
(2) must move forward with a velocity vtan.
(3) must move forward with a velocity vcos.
(4) should move in the backward direction.
A particle is thrown from the ground with a speed of 20 m/s at an angle 60° above the horizontal. Average velocity over its entire journey just before hitting the ground is:
(1) 10 m/s
(2) 20 m/s
(3) Zero
(4) 15 m/s
A person can throw a ball up to a maximum horizontal range of \(400~\text{m}\). The maximum height to which he can throw the ball is:
1. \(200~\text{m}\)
2. \(100~\text{m}\)
3. \(150~\text{m}\)
4. \(250~\text{m}\)
A car is moving along east at \(10\) m/s and a bus is moving along north at \(10\) m/s. The velocity of the car with respect to the bus is along:
| 1. | North-East | 2. | South-East |
| 3. | North-West | 4. | South-West |
A particle is moving on a circular path of radius 1m with a constant speed of 1 m/s. Acceleration of the particle is:
1.
2.
3.
4. 0
A particle starts moving from the origin in the XY plane and its velocity after time \(t\) is given by \(\overrightarrow{{v}}=4 \hat{{i}}+2 {t} \hat{{j}}\). The trajectory of the particle is correctly shown in the figure:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A particle is moving in the \(XY\) plane such that \(x = \left(t^2 -2t\right)~\text m,\) and \(y = \left(2t^2-t\right)~\text m,\) then:
| 1. | the acceleration is zero at \(t=1~\text s.\) |
| 2. | the speed is zero at \(t=0~\text s.\) |
| 3. | the acceleration is always zero. |
| 4. | the speed is \(3~\text{m/s}\) at \(t=1~\text s.\) |
Rain is pouring vertically downward at a velocity of \(4~\text{km/h}\). The magnitude of the velocity of rain with respect to a man running along the north on a horizontal road at \(3~\text{km/h}\) is:
1. \(7~\text{km/h}\)
2. \(5~\text{km/h}\)
3. \(1~\text{km/h}\)
4. \(3~\text{km/h}\)






