Maxwell's speed distribution graph is drawn as shown below. The most probable speed of the gas molecules is:
                        
1. 4 km/s

2. Between 3 km/s and 1 km/s

3. Any value between 2 km/s and 6 km/s

4. More than 4 km/s

A closed container having an ideal gas is heated gradually to increase the temperature by 20%  The mean free path will become/remain:

1. 20% more

2. Same

3. 20% less

4. 33% less

When the gas in an open container is heated, the mean free path:
1. Increases
2. Decreases
3. Remains the same
4. Any of the above depending on the molar mass

From the following V-T diagram, we can conclude

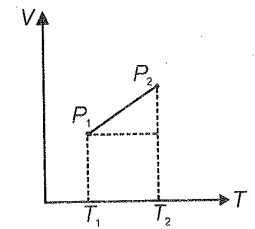
1. ${\mathrm{P}}_1$ = ${\mathrm{P}}_2$

2. ${\mathrm{P}}_1$ > ${\mathrm{P}}_2$

3. ${\mathrm{P}}_1$ < ${\mathrm{P}}_2$

4. ${\mathrm{P}}_1\ge {\mathrm{P}}_2$

How does the temperature change when the state of an ideal gas is changed according to the process shown in the figure?

What is the ratio of temperatures ${\mathrm{T}}_1 \mathrm{and} {\mathrm{T}}_2?$

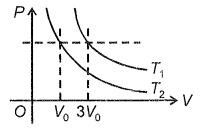
1. $\sqrt{3} :\hspace{0.17em}1$

2. 3 : 1

3. 9 : 1

4. 27 : 1

The mean free path for a gas, with molecular diameter \(d\) and number density \(n,\) can be expressed as:
1. \( \dfrac{1}{\sqrt{2} n \pi {d}^2} \)

2. \( \dfrac{1}{\sqrt{2} n^2 \pi {d}^2} \)

3. \(\dfrac{1}{\sqrt{2} n^2 \pi^2 d^2} \)

4. \( \dfrac{1}{\sqrt{2} n \pi {d}}\)

A cylinder contains hydrogen gas at a pressure of \(249~\text{kPa}\) and temperature \(27^\circ\text{C}.\) Its density is:
(\(R=8.3~\text{J mol}^{-1} \text {K}^{-1}\))
1. \(0.2~\text{kg/m}^{3}\)
2. \(0.1~\text{kg/m}^{3}\)
3. \(0.02~\text{kg/m}^{3}\)
4. \(0.5~\text{kg/m}^{3}\)