In the given figure, the spring balance is massless, so the reading of the spring balance will be:

| 1. | \(2\) kg | 2. | \(3.5\) kg |
| 3. | \(2.9\) kg | 4. | \(3.1\) kg |
When a body of mass \(m\) just begins to slide as shown, match List-I with List-II:
| List-I | List-II | ||
| (a) | Normal reaction | (i) | \(P\) |
| (b) | Frictional force \((f_s)\) | (ii) | \(Q\) |
| (c) | Weight \((mg)\) | (iii) | \(R\) |
| (d) | \(mg \mathrm{sin}\theta ~\) | (iv) | \(S\) |

Choose the correct answer from the options given below:
| (a) | (b) | (c) | (d) | |
| 1. | (ii) | (i) | (iii) | (iv) |
| 2. | (iv) | (ii) | (iii) | (i) |
| 3. | (iv) | (iii) | (ii) | (i) |
| 4. | (ii) | (iii) | (iv) | (i) |
A block of mass \(m\) is placed on a smooth inclined wedge \(ABC\) of inclination \(\theta\) as shown in the figure. The wedge is given an acceleration '\(a\)' towards the right. The relation between \(a\) and \(\theta\) for the block to remain stationary on the wedge is:
| 1. | \(a = \dfrac{g}{\mathrm{cosec }~ \theta}\) | 2. | \(a = \dfrac{g}{\sin\theta}\) |
| 3. | \(a = g\cos\theta\) | 4. | \(a = g\tan\theta\) |
Three blocks with masses \(m\), \(2m\), and \(3m\) are connected by strings as shown in the figure. After an upward force \(F\) is applied on block \(m\), the masses move upward at constant speed \(v\). What is the net force on the block of mass \(2m\)? (\(g\) is the acceleration due to gravity)

1. \(2mg\)
2. \(3mg\)
3. \(6mg\)
4. zero
The strings and pulleys shown in the figure are massless. The reading shown by the light spring balance \(S\) is:

| 1. | \(2.4\) kg | 2. | \(5\) kg |
| 3. | \(2.5\) kg | 4. | \(3\) kg |
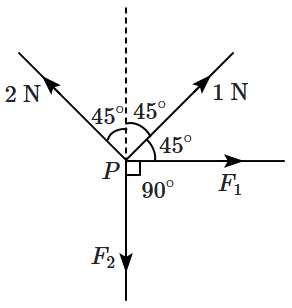
| 1. | \(4\) | 2. | \(3\) |
| 3. | \(2\) | 4. | \(1\) |
A rocket with a lift-off mass of \(20,000\) \(\mathrm{kg}\) is blasted upwards with an initial acceleration of \(5~\mathrm{ms}^{-2}\). Then initial thrust (force) of the blast is:
(Take \(g=10\) \(\mathrm{ms}^{-2}\))
1. \(7 \times 10^5 \mathrm{~N} \)
2. \(0 \)
3. \(2 \times 10^5 \mathrm{~N} \)
4. \(3 \times 10^5 \mathrm{~N}\)
A body of mass \(10 ~\text{Kg}\) is acted upon by two perpendicular forces, \(6 ~\text{N}\) and \(8 ~\text{N}.\) The resultant acceleration of the body is:
| (a) | \(1~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{4}{3}\right ) \) w.r.t. \(6 ~\text{N}\) force. |
| (b) | \(0.2~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{3}{4}\right ) \) w.r.t. \(8 ~\text{N}\) force. |
| (c) | \(1~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{3}{4}\right ) \) w.r.t. \(8 ~\text{N}\) force. |
| (d) | \(0.2~\text{ms}^{-2}\) at an angle of \(\text {tan}^{-1} \left(\dfrac{3}{4}\right ) \) w.r.t. \(6 ~\text{N}\) force. |
Choose the correct option from the given ones:
| 1. | (a) and (c) | 2. | (b) and (c) |
| 3. | (c) and (d) | 4. | (a), (b) and (c) |
(Take \(g=10\) m/s2)

1. \(\sqrt{390}\) m/s
2. \(\sqrt{410}\) m/s
3. \(20\) m/s
4. \(22\) m/s
The motion of a particle of mass \(m\) is described by \(y=ut+\frac{1}{2}gt^{2}.\) The force acting on the particle is:
1. \(3mg\)
2. \(mg\)
3. \(\frac{mg}{2}\)
4. \(2mg\)







