Q. No.The figure given below shows the displacement and time, \((x\text -t)\) graph of a particle moving along a straight line:
The correct statement, about the motion of the particle, is:
| 1. | the particle moves at a constant velocity up to a time \(t_0\) and then stops. |
| 2. | the particle is accelerated throughout its motion. |
| 3. | the particle is accelerated continuously for time \(t_0\) then moves with constant velocity. |
| 4. | the particle is at rest. |
1. \(1: \sqrt{3}\)
2. \(\sqrt{3}: 1\)
3. \(1:1\)
4. \(1:2\)
A particle moves a distance \(x\) in time \(t\) according to equation \(x = (t+5)^{-1}\). The acceleration of the particle is proportional to:
| 1. | \((\text{velocity})^{\frac{3}{2}}\) | 2. | \((\text{distance})^2\) |
| 3. | \((\text{distance})^{-2}\) | 4. | \((\text{velocity})^{\frac{2}{3}}\) |
1. \(1:1:1:1\)
2. \(1:2:3:4\)
3. \(1:4:9:16\)
4. \(1:3:5:7\)
A small block slides down on a smooth inclined plane starting from rest at time \(t=0.\) Let \(S_n\) be the distance traveled by the block in the interval \(t=n-1\) to \(t=n.\) Then the ratio \(\dfrac{S_n}{S_{n +1}}\) is:
| 1. | \(\dfrac{2n+1}{2n-1}\) | 2. | \(\dfrac{2n}{2n-1}\) |
| 3. | \(\dfrac{2n-1}{2n}\) | 4. | \(\dfrac{2n-1}{2n+1}\) |
When the velocity of a body is variable, then:
| 1. | its speed may be constant |
| 2. | its acceleration may be constant |
| 3. | its average acceleration may be constant |
| 4. | all of the above |
| 1. | \(68\) m | 2. | \(56\) m |
| 3. | \(60\) m | 4. | \(64\) m |
| 1. | \(- 2 nβ^{2} x^{- 2 n - 1}\) | 2. | \(- 2 nβ^{2} x^{- 4 n - 1}\) |
| 3. | \(- 2 \beta^{2} x^{- 2 n + 1}\) | 4. | \(- 2 nβ^{2} x^{- 4 n + 1}\) |
Which one of the following displacement-time graph represents two moving objects \(P\) and \(Q\) with zero relative velocity?
| 1. |  |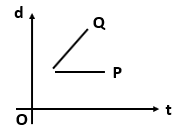
2. |  |
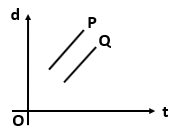| 3. |  |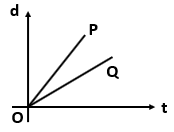
4. |  |
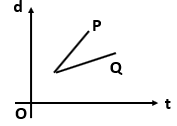If in one-dimensional motion, instantaneous speed \(v\) satisfies \(0\leq v<v_0,\) then:
| 1. | the displacement in time \(T\) must always take non-negative values. |
| 2. | the displacement \(x\) in time \(T\) satisfies \(-{v_0T} \lt x \lt {v_0T}.\) |
| 3. | the acceleration is always a non-negative number. |
| 4. | the motion has no turning points. |
© 2025 GoodEd Technologies Pvt. Ltd.