The relation between two specific heats (in cal/mol) of a gas is:
1.  ${\mathrm{C}}_{\mathrm{P}}-{\mathrm{C}}_{\mathrm{V}}=\frac{\mathrm{R}}{\mathrm{J}}$                               

2.  ${\mathrm{C}}_{\mathrm{V}}-{\mathrm{C}}_{\mathrm{P}}=\frac{\mathrm{R}}{\mathrm{J}}$

3.  ${\mathrm{C}}_{\mathrm{P}}-{\mathrm{C}}_{\mathrm{V}}=\mathrm{J}$                                 

4.  ${\mathrm{C}}_{\mathrm{V}}-{\mathrm{C}}_{\mathrm{P}}=\mathrm{J}$

The ratio of the specific heats \(\frac{C_P}{C_V}=\gamma\) in terms of degrees of freedom \((n)\) is given by:
1. \(1+1/n\)
2. \(1+n/3\)
3. \(1+2/n\)
4. \(1+n/2\)

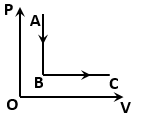
The figure shows a process for a gas in which pressure (P) and volume (V) of the gas change. If $C_1$ and $C_2$ are the molar heat capacities of the gas during the processes AB and BC respectively, then:

1. $C_1=C_2$

2. $C_1>C_2$

3. $C_1<C_2$

4. $C_1\le C_2$

The specific heat of an ideal gas is:

1.  proportional to $\mathrm{T.}$                     

2.  proportional to T².

3.  proportional to T³.                  

4.  independent of $\mathrm{T.}$

If \(C_P\) and \(C_V\) denote the specific heats (per unit mass) of an ideal gas of molecular weight \(M\) (where \(R\) is the molar gas constant), the correct relation is:
1. \(C_P-C_V=R\)
2. \(C_P-C_V=\frac{R}{M}\)
3. \(C_P-C_V=MR\)
4. \(C_P-C_V=\frac{R}{M^2}\)

For hydrogen gas, the difference between molar specific heats is given by; \(C_P-C_V=a,\) and for oxygen gas, \(C_P-C_V=b.\) Here, \(C_P\)​ and \(C_V\)​ are molar specific heats expressed in \(\text{J mol}^{-1}\text{K}^{-1}.\) What is the relationship between \(a\) and \(b?\)
1. \(a=16b\)
2. \(b=16a\)
3. \(a=4b\)
4. \(a=b\)

The specific heat of a gas:

The value of $C_P-C_v=1.00$ $R$ for a gas in state A and $C_P-C_v=1.06$ $R$ in another state B. If $P_A$ $and$ $P_B$ denote the pressure and $T_A\&$ $T_B$ denote the temperatures in the two states, then:

The amount of heat energy required to raise the temperature of \(1\) g of Helium at NTP, from \({T_1}\) K to \({T_2}\) K is:
1. \(\frac{3}{2}N_ak_B(T_2-T_1)\)
2. \(\frac{3}{4}N_ak_B(T_2-T_1)\)
3. \(\frac{3}{4}N_ak_B\frac{T_2}{T_1}\)
4. \(\frac{3}{8}N_ak_B(T_2-T_1)\)