The kinetic energy acquired by a mass m in travelling a certain distance d starting from rest under the action of a constant force is directly proportional to 

(1) $\sqrt{m}$

(2) Independent of m

(3) $1/\sqrt{m}$

(4) m

An open knife edge of mass 'm' is dropped from a height 'h' on a wooden floor. If the blade penetrates upto the depth 'd' into the wood, the average resistance offered by the wood to the knife edge is 

(1) mg

(2) $mg\left(1-\frac{{\displaystyle h}}{{\displaystyle d}}\right)$

(3) $mg\left(1+\frac{{\displaystyle h}}{{\displaystyle d}}\right)$

(4) $mg{\left(1+\frac{{\displaystyle h}}{{\displaystyle d}}\right)}^2$

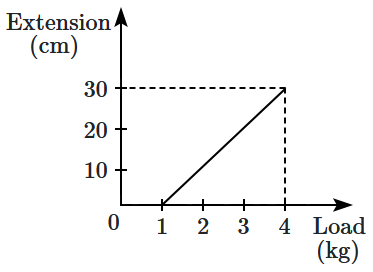
1. \(0.1\text{ N/cm}\)

2. \(5\text{ N/cm}\)

3. \(0.3\text{ N/cm}\)

4. \(1\text{ N/cm}\)

A particle which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as $F\left(x\right)=-kx+a{x}^3$. Here k and a are positive constants. For $x\ge 0$, the functional form of the potential energy U(x) of the particle is-

(1)

(2)

(3)

(4)

The force acting on a body moving along x-axis varies with the position of the particle as shown in the fig.

The body is in stable equilibrium at

1. x = x₁

2. x = x₂

3. both x₁ and x₂

4. neither x₁ nor x₂

A particle is placed at the origin and a force F = kx is acting on it (where k is positive constant). If U(0) = 0, the graph of U(x) versus x will be (where U is the potential energy function) 

1. 

2. 

3. 

4. 

A body of mass 1 kg begins to move under the action of a time dependent force \(F = 2 t\) \(\hat{i} + 3 t^{2}\ \hat{j}\) N, where \(\hat{i}\) and \(\hat{j}\) are unit vectors along X and Y axis, What power will be developed by the force at the time (t) ?

1. \(\left(2 t^{2} + 4 t^{4}\right) W\)         

2. \(\left(2 t^{3} + 3 t^{4}\right) W\)

3. \(\left(2 t^{3} + 3 t^{5}\right) W\)         

4. \(\left(2 t + 3 t^{3}\right) W\)

A particle of mass m is driven by a machine that delivers a constant power of k watts. If the particle starts from rest the force on the particle at time t is:

1. $\sqrt{\left(\frac{mk}{2}\right)}{t}^{-1/2}$
 

2. $\sqrt{\left(mk\right)}{t}^{-1/2}$
 

3. $\sqrt{\left(2mk\right)}{t}^{-1/2}$
 

4. $\frac{1}{2}\sqrt{\left(mk\right)}{t}^{-1/2}$

Two particles of masses m₁,m₂ move with initial velocities u₁ and u₂. On collision, one of the particles get excited to higher level, after absorbing energy $\epsilon$. If final velocities of particles be v₁ and v₂, then we must have

1. m₁²u₁+m₂²u₂-$\epsilon$=m₁²v₁+m₂²v₂

2. $\frac{1}{2}$m₁u₁²+$\frac{1}{2}$m₂u₂=$\frac{1}{2}$m₁v₁²+$\frac{1}{2}$m₂v₂²-$\epsilon$

3. $\frac{1}{2}$m₁u₁²+$\frac{1}{2}$m₂u₂²-$\epsilon$=$\frac{1}{2}$m₁v₁²+$\frac{1}{2}$m₂v₂²

4. $\frac{1}{2}$m₁²u₁²+$\frac{1}{2}$m₂²u₂²+$\epsilon$=$\frac{1}{2}$m₁²v₁²+$\frac{1}{2}$m₂²v₂²
 

A ball is thrown vertically downwards from a height of \(20\) m with an initial velocity \(v_0\). It collides with the ground, loses \(50\%\) of its energy in a collision and rebounds to the same height. The initial velocity \(v_0\) is: (Take \(g = 10~\text{m/s}^2\))
1. \(14~\text{m/s}\)
2. \(20~\text{m/s}\)
3. \(28~\text{m/s}\)
4. \(10~\text{m/s}\)