Select Question Set:
Q. No.A uniform rod is pivoted at one of its ends, so that it can rotate freely in a vertical plane. Initially, it hangs vertically as shown in the figure. A sharp impulse is delivered to the rod at its lowest end \(B,\) towards the right. An impulse is exerted by the pivot at \(A,\) due to the constraint. The impulse at \(A\) acts:
1. to the right.
2. to the left.
3. upward.
4. downward.
Subtopic: Application of Laws |
Level 3: 35%-60%
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
A block of mass \(m\) is placed between two springs connected to the ends of a railroad car. The surface supporting the block is horizontal, and the spring are initially relaxed. The car is given an acceleration \(a\) and the mass \(m\) finally comes to equilibrium within the car. Let \(x\) be the compression (or extension) in the two springs. Assume friction to be negligible. Then:
| 1. | \(k_1x-k_2x=ma \) |
| 2. | \(\dfrac{k_1k_2}{k_1+k_2}x=ma \) |
| 3. | \(k_1x+k_2x=ma \) |
| 4. | \(\dfrac{k_1k_2}{k_1-k_2}=ma \) |
Subtopic: Spring Force |
57%
Level 3: 35%-60%
Hints
The two blocks \(A,~B\) are connected by an inextensible string, and are lying on a horizontal surface. The blocks move under the action of forces of magnitudes \(F_1\) and \(F_2,\) as shown in the figure. The surface exerts non-zero frictional forces \(f_A,~f_B\) (towards right).
Consider the following situations:
Which of the above, are possible? Assume that the string is taut.
1. (P) or (Q)
2. (R) or (S)
3. Any of (P), (Q), (R), (S)
4. Only (P)
Consider the following situations:
| (P) | \(f_A,~f_B>0\) | (Q) | \(f_A,~f_B<0\) |
| (R) | \(f_A>0,~ f_B<0\) | (S) | \(f_A<0,~ f_B>0\) |
Which of the above, are possible? Assume that the string is taut.
1. (P) or (Q)
2. (R) or (S)
3. Any of (P), (Q), (R), (S)
4. Only (P)
Subtopic: Friction |
Level 3: 35%-60%
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
A block of mass \(m\) is placed on a flat horizontal surface, and the coefficient of friction between the block and the surface is \(\mu\). A force \(F_A\) is applied to the block from above, and a force \(F_R\) is applied to the right. In all situations being considered below, the block remains at rest. Let \(f\) be the force of friction on the block.
Consider the statements:
1. Only P is True.
2. Only Q is True.
3. P, Q are True.
4. Only R is True.
Consider the statements:
| (P) | \(f\) increases if \(m\) is increased. |
| (Q) | \(f\) increases if \(F_A\) is increased. |
| (R) | \(f\) increases if \(F_R\) is increased. |
2. Only Q is True.
3. P, Q are True.
4. Only R is True.
Subtopic: Friction |
Level 3: 35%-60%
Hints
A small block of mass \(m\) is released as shown in the figure against the vertical part of the smooth curved surface of a wedge of mass \(M\), initially at rest. When the block reaches the bottom, it travels horizontally with a kinetic energy \(E_m,\) while the wedge recoils towards left with a kinetic energy \(E_M.\) Then:
| 1. | \(\dfrac{E_m}{m}=\dfrac{E_M}{M}\) | 2. | \(mE_m=ME_M\) |
| 3. | \(\dfrac{E_m}{m^2}=\dfrac{E_M}{M^2}\) | 4. | \(m^2E_m=M^2E_M\) |
Subtopic: Application of Laws |
68%
Level 2: 60%+
Hints
A box is moving down a frictionless \(30^{\circ}\) incline, and a particle is projected within the box. The acceleration of the particle relative to the box is:
1. \(g\)
2. \(g~\text{sin}30^{\circ}\)
3. \(g~\text{cos}30^{\circ}\)
4. \(g~\text{tan}30^{\circ}\)
1. \(g\)
2. \(g~\text{sin}30^{\circ}\)
3. \(g~\text{cos}30^{\circ}\)
4. \(g~\text{tan}30^{\circ}\)
Subtopic: Application of Laws |
Level 3: 35%-60%
Hints
An Atwood's machine with blocks of masses \(3\) kg and \(2\) kg is set up in a laboratory. The string is taut and the blocks start moving at \(t=0.\)
The relative acceleration of the blocks has the magnitude:
1. \(\dfrac{g}{5}\)
2. \(\dfrac{2g}{5}\)
3. \(\dfrac{3g}{5}\)
4. \(\dfrac{4g}{5}\)
The relative acceleration of the blocks has the magnitude:
1. \(\dfrac{g}{5}\)
2. \(\dfrac{2g}{5}\)
3. \(\dfrac{3g}{5}\)
4. \(\dfrac{4g}{5}\)
Subtopic: Application of Laws |
52%
Level 3: 35%-60%
Hints
An Atwood's machine with blocks of masses \(3\) kg and \(2\) kg is set up in a laboratory. The string is taut and the blocks start moving at \(t=0.\)
The work done by tension on the \(3\) kg block has a magnitude \(W_1\) while the work done by gravity on the same block has a magnitude \(W_2,\) since the beginning of motion.
The work done by tension on the \(3\) kg block has a magnitude \(W_1\) while the work done by gravity on the same block has a magnitude \(W_2,\) since the beginning of motion.
| 1. | \(W_1=W_2\) |
| 2. | \(W_1>W_2\) |
| 3. | \(W_1<W_2\) |
| 4. | Any of the above can be true |
Subtopic: Application of Laws |
54%
Level 3: 35%-60%
Hints
A block of height \(h\) and width \(w\) is placed on a horizontal table. A horizontal force \(F\) is applied parallel to the top surface of the block. The block does not slip due to friction. Let the frictional force on the block be \(f\) and the normal reaction of the table on the block be \(N.\) Then,
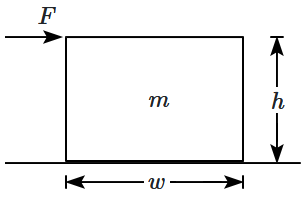
| 1. | \(N\) increases as \(F\) increases. |
| 2. | \(N\) does not act through the center of the block. |
| 3. | \(f\) is greater than \(F.\) |
| 4. | \(f\) acts through the centre of the block. |
Subtopic: Friction |
Level 3: 35%-60%
Hints
A balloon ascending with an acceleration \(a\) has a ballast of mass \(m\) thrown out, and it is observed to move upward with double the acceleration. The mass of the remaining part (after the ballast is thrown out) is:
| 1. | \(m\dfrac{g+2a}{g+a}\) |
| 2. | \(m\dfrac{g+a}{g}\) |
| 3. | \(m\dfrac{g+a}{a}\) |
| 4. | \(m\dfrac{g+2a}{g}\) |
Subtopic: Newton's Laws |
52%
Level 3: 35%-60%
Hints
Select Question Set:
© 2025 GoodEd Technologies Pvt. Ltd.