Select Question Set:
An equi-convex lens of focal length \(20\) cm (in the air) is split into two parts by a surface that has half the curvature of either of its outer surfaces. The ratio of the powers of the two lenses thus formed is:
1. \(3:1\)
2. \(2:1\)
3. \(1:1\)
4. \(-2:1\)
Subtopic: Lenses |
Level 4: Below 35%
Hints
An equi-convex lens of focal length \(50~\text{cm}\) and an equi-concave lens of the same focal length are placed \(50~\text{cm}\) apart, with a common principal axis. A point object is placed on the principal axis of the system, at a distance of \(100~\text{cm}\) in front of the convex lens (see figure). The final image is formed at:


| 1. | \(100~\text{cm}\) in front of the concave lens |
| 2. | \(50~\text{cm}\) in front of the concave lens |
| 3. | \(50~\text{cm}\) behind the concave lens |
| 4. | infinity |
Subtopic: Lenses |
58%
Level 3: 35%-60%
Hints
A plano-convex lens made of glass \((\mu=1.5)\) is placed with its convex surface in a liquid, and it is found that the focal length is doubled. The refractive index of the liquid is:
1. \(3\)
2. \(2\)
3. \(1.25\)
4. \(1.2\)
1. \(3\)
2. \(2\)
3. \(1.25\)
4. \(1.2\)
Subtopic: Lenses |
50%
Level 3: 35%-60%
Hints
A thin prism of refractive index \(\mu = 1.5\) introduces a deviation of \(+1^\circ\) into the path of an incident beam. When this prism is immersed in a liquid of refractive index \(\mu = 2\), the deviation introduced will be:
| 1. | \( \left ( \dfrac{7}{6} \right )^\circ\) | 2. | \( \left ( \dfrac{3}{2} \right )^\circ\) |
| 3. | \(- \left ( \dfrac{1}{2} \right )^\circ\) | 4. | \( \left ( \dfrac{1}{2} \right )^\circ\) |
Subtopic: Prisms |
60%
Level 2: 60%+
Hints
Calculate the dispersive power of a thin prism from the following data:
1. \(0.04\)
2. \(0.02\)
3. \(25\)
4. \(50\)
| Colour | Deviation | ||
| Violet | \(2.04^\circ\) | ||
| Yellow | \(2.00^\circ\) | ||
| Red | \(1.96^\circ\) |
2. \(0.02\)
3. \(25\)
4. \(50\)
Subtopic: Prisms |
77%
Level 2: 60%+
Hints
A parallel beam of light is incident onto a convex lens and after passing through the lens, it gets reflected from a plane mirror and passes through the lens again. The focal length of the lens is \(f.\) Where should the mirror be placed so that the final beam emerges parallel?
| 1. | Just behind the lens. |
| 2. | At the focus of the lens. |
| 3. | At a distance of \(2f\) from the lens. |
| 4. | At a distance of \(3f\) from the lens. |
Subtopic: Lenses |
68%
Level 2: 60%+
Hints
An equiconvex lens of focal length \(50\) cm is made of glass of refractive index, \(\mu=1.5.\) It is split into two identical plano-convex lenses, and a glass-slab of the same refractive index, and of thickness \(300\) cm is inserted between the two half-lenses (plano-convex). When a parallel beam is incident on the combination, the emerging beam:
| 1. | focuses at a distance of \(100\) cm from the second lens. |
| 2. | focuses at \(200\) cm from second lens. |
| 3. | focuses at \(150\) cm from second lens. |
| 4. | emerges as a parallel beam. |
Subtopic: Lenses |
Level 3: 35%-60%
Hints
An equiconvex lens of focal length \(100\) cm is split into two plano-convex lenses and the plane surface of one of these lenses is silvered. This acts as a:
| 1. | converging mirror of focal length \(200\) cm. |
| 2. | converging mirror of focal length \(100\) cm. |
| 3. | diverging mirror of focal length \(200\) cm. |
| 4. | diverging mirror of focal length \(100\) cm. |
Subtopic: Lenses |
Level 3: 35%-60%
Hints
Two identical equilateral triangular prisms, each of which gives a minimum deviation of \(60^{\circ}\) are taken: call these prisms \(A,B\). These are placed as shown in the figure, and a ray of light is incident on prism \(A\) at minimum deviation. Now prism \(B\) is cut in half, along the dotted line, and the right half is removed. The deviation of the emerging ray is:


| 1. | \(90^{\circ}\) | 2. | \(45^{\circ}\) |
| 3. | \(60^{\circ}\) | 4. | \(30^{\circ}\) |
Subtopic: Prisms |
50%
Level 3: 35%-60%
Hints
A thin plane parallel slab (thickness \(t\), refractive index \(\mu\)) is placed just behind a converging lens of focal length \(f.\) If a parallel beam of light is incident on the combination it will converge at a distance of:
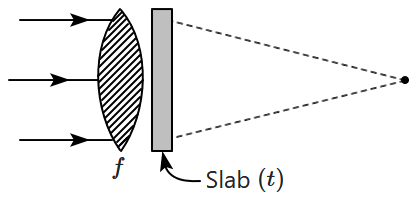

| 1. | \(f\) from the end of the slab. |
| 2. | \(f-\frac{t}{\mu}\) from the end of the slab. |
| 3. | \(f+\frac{t}{\mu}\) from the end of the slab. |
| 4. | \(f+t\Big(1-\frac{1}{\mu}\Big)\) from the end of the slab. |
Subtopic: Refraction at Curved Surface |
Level 4: Below 35%
Hints
Select Question Set:






