An infinitely long straight conductor carries a current of \(5~\text{A}\) as shown. An electron is moving with a speed of \(10^5~\text{m/s}\) parallel to the conductor. The perpendicular distance between the electron and the conductor is \(20~\text{cm}\) at an instant. Calculate the magnitude of the force experienced by the electron at that instant.

1.
\(4\pi\times 10^{-20}~\text{N}\)
2.
\(8\times 10^{-20}~\text{N}\)
3.
\(4\times 10^{-20}~\text{N}\)
4.
\(8\pi\times 10^{-20}~\text{N}\)

A uniform conducting wire of length \(12a\) and resistance '\(R\)' is wound up as a current-carrying coil in the shape of;
| (i) | an equilateral triangle of side '\(a\)' |
| (ii) | a square of side '\(a\)' |
The magnetic dipole moments of the coil in each case respectively are:
1. \(3Ia^2~\text{and}~4Ia^2\)
2. \(4Ia^2~\text{and}~3Ia^2\)
3. \(\sqrt{3}Ia^2~\text{and}~3Ia^2\)
4. \(3Ia^2~\text{and}~Ia^2\)
In the product
\(\vec{F}=q\left ( \vec{v}\times \vec{B} \right )\)
\(~~~=q\vec{v}\times \left ( B\hat{i}+B\hat{j}+B_0\hat{k} \right )\)
For \(q=1\) and \(\vec{v}=2\hat{i}+4\hat{j}+6\hat{k}\)
and \(\vec{F}=4\hat{i}-20\hat{j}+12\hat{k}\)
What will be the complete expression for \(\vec{B}\)?
1. \(8\hat{i}+8\hat{j}-6\hat{k}\)
2. \(6\hat{i}+6\hat{j}-8\hat{k}\)
3. \(-8\hat{i}-8\hat{j}-6\hat{k}\)
4. \(-6\hat{i}-6\hat{j}-8\hat{k}\)
A thick current-carrying cable of radius '\(R\)' carries current \('I'\) uniformly distributed across its cross-section. The variation of magnetic field \(B(r)\) due to the cable with the distance '\(r\)' from the axis of the cable is represented by:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
A circular loop of area \(1\) cm2, carrying a current of \(10\) A, is placed in a magnetic field of \(0.1\) T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is:
1. zero
2. \(10^{-4}\) N-m
3. \(10^{-2}\) N-m
4. \(1\) N-m
A current-carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
| 1. | will exert an inward force on the circular loop |
| 2. | will exert an outward force on the circular loop |
| 3. | will not exert any force on the circular loop |
| 4. | will exert a force on the circular loop parallel to itself |
A long, straight wire carries a current along the \(z-\)axis. One can find two points in the \(X-Y\) plane such that:
| (a) | the magnetic fields are equal |
| (b) | the direction of the magnetic fields are the same |
| (c) | the magnitude of the magnetic fields are equal |
| (d) | the field at one point is opposite to that at the other point |
Choose the correct option :
| 1. | (a), (b), (c) | 2. | (b), (c), (d) |
| 3. | (c), (d), (a) | 4. | all of the above |
| 1. | \( \dfrac{{IL}^2}{4} ~\text{A}\text-\text{m}^2 \) | 2. | \( \dfrac{{I} \times \pi {L}^2}{4} ~\text{A}\text-\text{m}^2 \) |
| 3. | \( \dfrac{2 {IL}^2}{\pi}~\text{A}\text-\text{m}^2 \) | 4. | \( \dfrac{{IL}^2}{4 \pi}~\text{A}\text-\text{m}^2 \) |
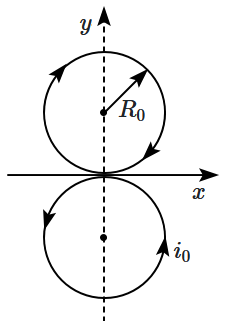
| 1. | \(\left({{i}_{0}\mathit{\pi}{R}_{0}^{2}}\right)\sqrt{2} \) | 2. | zero |
| 3. | \({i}_{0}\times{2}\mathit{\pi}{R}_{0}^{2} \) | 4. | \({i}_{0}\left({{4}\mathit{\pi}{R}_{0}}\right) \) |
| 1. | field is the same every where around the conductor. |
| 2. | field is directly proportional to the square of the current flowing in the conductor. |
| 3. | field obeys the inverse square law of distance. |
| 4. | magnetic field strength was maximum on the axis of the current conductor. |






