The frequency of oscillation of a mass m suspended by a spring is ${\mathrm{\nu }}_1$. If the length of the spring is cut to one third, then the same mass oscillates with a frequency ${\mathrm{\nu }}_2$_, then:

(1) ${\mathrm{\nu }}_2$ = 3${\mathrm{\nu }}_1$

(2) 3${\mathrm{\nu }}_2$ = ${\mathrm{\nu }}_1$

(3) ${\mathrm{\nu }}_2$ = $\sqrt{3}$${\mathrm{\nu }}_1$

(4) $\sqrt{3}$${\mathrm{\nu }}_2$ = ${\mathrm{\nu }}_1$

The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in the figure. The time period of osciliation of the particle is:

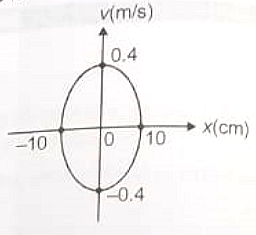
(1) $\frac{\pi }{2} \mathrm{s}$

(2) $\pi$ s

(3) 2$\pi$ s

(4) 3$\pi$ s

The equation of simple harmonic motion may not be expressed as (each term has its usual meaning):

(1) $x=A\sin (\omega t+\varphi )$

(2) $x=A\cos (\omega t-\varphi )$

(3) $x=a\sin \omega t + b\cos \omega t$

(4) $x=A\sin (\omega t+\varphi )+B\sin (2\omega t+\varphi )$

If a particle is executing simple harmonic motion, then the acceleration of the particle:

(1) is uniform.

(2) varies linearly with time.

(3) is non-uniform.

(4) Both (2) & (3)

What is the phase difference between the acceleration and the velocity of a particle executing simple harmonic motion?

(1) Zero

(2) $\frac{\pi }{2}$

(3) $\pi$

(4) 2$\pi$

The shape of the graph plotted between the velocity and the position of a particle executing simple harmonic motion is:

(1) A straight line

(2) An ellipse

(3) A parabola

(4) A hyperbola 

If a particle is executing simple harmonic motion with time period T, then the time period of its total mechanical energy is:

(1) Zero

(2) $\frac{T}{2}$

(3) 2T

(4) Infinite

Select the wrong statement about simple harmonic motion.

(1) The body is uniformly accelerated.

(2) The velocity of the body changes smoothly at all instants.

(3) The amplitude of oscillation is symmetric about the equilibrium position.

(4) The frequency of oscillation is independent of amplitude.

A particle is executing SHM with time period T starting from the mean position. The time taken by it to complete $\frac{5}{8}$ oscillations is:

(1) $\frac{T}{12}$

(2) $\frac{T}{6}$

(3) $\frac{5T}{12}$

(4) $\frac{7T}{12}$

A particle is executing S.H.M. between x = $\pm$ A. The time taken to go from 0 to $\frac{A}{2}$ is T₁ and to go from $\frac{A}{2}$ to A is T_2, then:

(1) T₁ < T₂

(2) T₁ > T₂

(3) T₁ = T₂

(4) T₁ = 2T₂