A particle is executing SHM with time period T starting from the mean position. The time taken by it to complete $\frac{5}{8}$ oscillations is:

(1) $\frac{T}{12}$

(2) $\frac{T}{6}$

(3) $\frac{5T}{12}$

(4) $\frac{7T}{12}$

A particle is executing S.H.M. between x = $\pm$ A. The time taken to go from 0 to $\frac{A}{2}$ is T₁ and to go from $\frac{A}{2}$ to A is T_2, then:

(1) T₁ < T₂

(2) T₁ > T₂

(3) T₁ = T₂

(4) T₁ = 2T₂

For a particle executing simple harmonic motion, the amplitude is A and the time period is T. The maximum speed will be:

(1) 4AT

(2) $\frac{2A}{T}$

(3) $2\pi \sqrt{\frac{A}{T}}$

(4) $\frac{2\pi A}{T}$

A particle is executing S.H.M with an amplitude A and has maximum velocity v_0, its speed at displacament $\frac{3\mathrm{A}}{4}$ will be:

(1) $\frac{\sqrt{7}}{4}{v}_0$

(2) $\frac{v_0}{\sqrt{2}}$

(3) v₀

(4) $\frac{\sqrt{3}}{2}{v}_0$

Two particles executing SHM of the same frequency meet at x = +a/2 while moving in opposite directions. The phase difference between the particles is:

(1) $\frac{\pi }{6}$

(2) $\frac{\mathrm{\pi }}{3}$

(3) $\frac{5\mathrm{\pi }}{6}$

(4) $\frac{2\mathrm{\pi }}{3}$

The displacements of two particles executing SHM on the same line are given as
${\mathrm{y}}_1=asin\left(\frac{\mathrm{\pi }}{2}\mathrm{t}+\mathrm{\varphi }\right)$ and ${\text{y}}_2=\mathrm{bsin}\left(\frac{2\mathrm{\pi }}{3}\mathrm{t}+\mathrm{\varphi }\right)$. The phase difference between them at t=1 sec is:

(1) $\mathrm{\pi }$

(2) $\frac{\pi }{2}$

(3) $\frac{\pi }{4}$

(4) $\frac{\pi }{6}$

For a particle showing motion under the force F= -5 (x - 2)², the motion is:

(1) Translatory

(2) Oscillatory

(3) SHM

(4) All of these

For a particle showing motion under the force F= -5(x - 2), the motion is:

(1) Translatory

(2) Oscillatory

(3) SHM

(4) Both (2) & (3)

Two identical springs have the same force constant 73.5 Nm^-1. The elongation produced in each spring in three cases shown in Figure-1, Figure- 2 and Figure- 3 are: (g = 9.8 ms^-2)

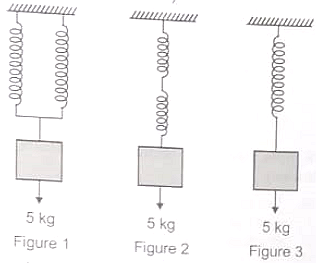
(1) $\frac{1}{6}m,\frac{2}{3}m,\frac{1}{3}m$

(2) $\frac{1}{3}m,\frac{1}{3}m,\frac{1}{3}m$

(3) $\frac{2}{3}m,\frac{1}{3}m,\frac{1}{6}m$

(4) $\frac{1}{3}m,\frac{4}{3}m,\frac{2}{3}m$

A particle of mass 10 g is undergoing SHM of amplitude 10 cm and period 0.1 sec. The maximum value of the force on the particle is about:

(1) 5.6 N

(2) 2.75 N

(3) 3.5 N

(4) 4 N