A particle moves along a path \(ABCD\) as shown in the figure. The magnitude of the displacement of the particle from \(A\) to \(D\) is:
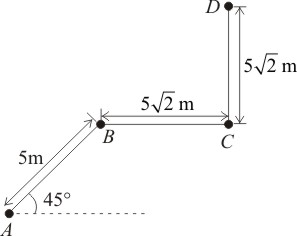
1. m
2. \(10\) m
3. m
4. \(15\) m

2. \(10\) m
3. m
4. \(15\) m
The velocity of a particle moving along a straight line with constant acceleration \(a\) reduces to \(\frac{1}{5}\) of its initial velocity in time \(\tau.\) The total time taken by the body till its velocity becomes zero is:
1. \(\frac{4\tau}{3}\)
2. \(\frac{5\tau}{4}\)
3. \(\frac{4\tau}{5}\)
4. \(\frac{3\tau}{4}\)
A boy falls from a building of height \(320\) m. After \(5\) seconds, superman jumps downward with initial speed \(u\) such that the boy can be saved. The minimum value of \(u\) is: (assume \(g= 10~\text{m/s}^2\))
| 1. | \(95.1\) m/s | 2. | \(98.3\) m/s |
| 3. | \(91.6\) m/s | 4. | \(85.6\) m/s |
The displacement \(x\) of a body having relation with time as \(x = 3t^2 -6t+7,\) then distance covered by body in first two second is [where \(x\) is in metre and \(t\) is in second].
1. Zero
2. \(6\) m
3. \(3\) m
4. \(9\) m
| 1. | \(\dfrac{1}{v} = \dfrac{1}{v_1}+\dfrac{1}{v_2}\) | 2. | \(\dfrac{2}{v} = \dfrac{1}{v_1}+\dfrac{1}{v_2}\) |
| 3. | \(\dfrac{v}{2} = \dfrac{v_1+v_2}{2}\) | 4. | \(v = \sqrt{v_1v_2}\) |
| 1. | \(t_1<t_2 \) or \(t_1>t_2 \) depending upon whether the lift is going up or down. |
| 2. | \(t_1<t_2 \) |
| 3. | \(t_1>t_2 \) |
| 4. | \(t_1=t_2 \) |
\((g = 10~\text{m/s}^2)\)
1. \(35~\text{m}\)
2. \(45~\text{m}\)
3. \(80~\text{m}\)
4. \(20~\text{m}\)
The acceleration of particle for which the versus s graph is shown is:
1. - 8
2. 4
3. - 4
4. -16
| Assertion (A): | A body is momentarily at rest when it reverses the direction of motion. |
| Reason (R): | A body cannot have acceleration if its velocity is zero at a given instant of time. |
| 1. | Both (A) and (R) are true and (R) is the correct explanation of (A). |
| 2. | Both (A) and (R) are true but (R) is not the correct explanation of (A). |
| 3. | (A) is true but (R) is false. |
| 4. | (A) is false but (R) is true. |
The position (x) of a particle moving along x-axis varies with time (t) as . The particle turns around at
1. t=1 s
2. t=2 s
3. t=3 s
4. t=4 s





