The gravitational field due to a mass distribution is given by $\overrightarrow{I}=<mspace\; width="1em"></mspace>\frac{k}{x^2}\hat{i}$, where k is a constant. Assuming the potential to be zero at infinity, find the potential at a point x = a.[This question includes concepts from Gravitation chapter]

1. $\frac{k}{a^2}$

2. $\frac{-k}{a^2}$

3. $\frac{k}{a}$

4. $\frac{-k}{a}$

The gravitational potential difference between the surface of a planet and 10 m above is 5 J/kg. If the gravitational field is supposed to be uniform, the work done in moving a 2 kg mass from the surface of the planet to a height of 8 m is

1.  2J

2.  4J

3.  6J

4.  8J

Four particles each of mass M, are located at the vertices of a square with side L. The

gravitational potential due to this at the centre of the square is

1. $-\sqrt{32}\frac{GM}{L}$                                   

2. $-\sqrt{64}\frac{GM}{L^2}$

3. zero                                             

4. $\sqrt{32}\frac{GM}{L}$

The gravitational field due to a mass distribution is $E=K/x^3$ in the x-direction. (K is a

constant). Taking the gravitational potential to be zero at infinity, its value at a distance x

is

1. K/x                    

2. K/2x

3. $K/x^2$                 

4. K/2$x^2$

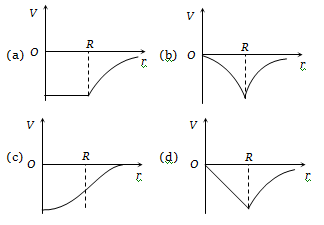
The diagram showing the variation of gravitational potential of earth with distance r from the centre of earth is -

 

1.		2.
3.		4.

At what height from the surface of earth the gravitation potential and the value of g are $-5.4\times {10}^{7}J$ $k{g}^{-2}$ and $6.0$ $m{s}^{-2}$ respectively? (Take, the radius of earth as 6400 km.)

1. 1600 km             
2. 1400 km 
3. 2000 km             
4. 2600 km

Infinite number of bodies, each of mass 2 kg are situated on x-axis at distance 1m, 2m,  4m, 8m, respectively from the origin. The resulting gravitational potential due to this system at the origin will be

1. -G

2. -8/3G

3. -4/3G

4. -4G

A particle of mass M is situated at the centre of a spherical shell of mass M and radius a.The gravitational potential at a point situated at a/2 distance from the centre will be 

1. $-\frac{3GM}{a}$                                       2. $-\frac{2GM}{a}$

3. $-\frac{GM}{a}$                                         4. $-\frac{4GM}{a}$

Mass and radius of the earth is M and R respectively, then the gravitational potential at a distance R/3 from the centre of the earth is

1.  $-\frac{\mathrm{GM}}{\mathrm{R}}$

2.  $-\frac{3\mathrm{GM}}{\mathrm{R}}$

3.  $-\frac{11}{9}\frac{\mathrm{GM}}{\mathrm{R}}$

4.  $-\frac{13}{9}\frac{\mathrm{GM}}{\mathrm{R}}$