A particle is projected at an angle $\theta$ with horizontal with an initital speed u. When it makes an angle $\alpha$ with horizontal, its speed v is-

1. $u\cos \theta$

2. $u\cos \theta <mspace\; width="1em"></mspace>u\cos \alpha$

3. $\frac{u\sin \theta }{\sin \alpha }$

4. $\frac{u\cos \theta }{\cos \alpha }$

A body is projected with velocity $20\sqrt{3}$ m/s with an angle of projection 60$°$ with horizontal. Calculate velocity on that point where body makes an angle 30$°$ with the horizontal.

1. 20 m/s

2. $\frac{20}{\sqrt{3}}<mspace\; width="1em"></mspace>m/s$

3. $10\sqrt{3}<mspace\; width="1em"></mspace>m/s$

4. 10 m/s

A particle is projected with a velocity u making an angle $\mathrm{\theta }$ with the horizontal. At any instant, its velocity v is at right angles to its initial velocity u; then v is:

1.  ucos$\mathrm{\theta }$

2.  utan$\mathrm{\theta }$

3.  ucot$\mathrm{\theta }$

4.  usec$\mathrm{\theta }$

A projectile is given an initial velocity of $\hat{i}+2\hat{j}$. The cartesian equation of its path is (g = 10 ${\mathrm{ms}}^{-2}$) 

1. $\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

2. $\mathrm{y}=\mathrm{x}-5{\mathrm{x}}^2$

3. $4\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

4. $\mathrm{y}=2\mathrm{x}-25{\mathrm{x}}^2$

Time taken by the projectile to reach from A to B is t. Then the distance AB is equal to :

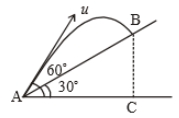
1. $\frac{ut}{\sqrt{3}}$

2. $\frac{\sqrt{3}ut}{2}$

3. $\sqrt{3}ut$

4. 2ut

A particle projected with kinetic energy ${\mathrm{k}}_0$ with an angle of projection $\mathrm{\theta }$. Then the variation of kinetic K with vertical displacement y is

1.  linear

2.  parabolic

3.  hyperbolic

4.  periodic

 A body is thrown horizontally with a velocity \(\sqrt{2 g h}\) from the top of a tower of height \(h\). It strikes the level ground through the foot of the tower at a distance \(x\) from the tower. The value of \(x\) is:

A body is projected with a velocity \(u\) with an angle of projection \(\theta.\) The change in velocity after the time \((t)\) from the time of projection will be:

What determines the nature of the path followed by the particle?

1. Speed only

2. Velocity only

3. Acceleration only

4. None of these

A ball P is dropped vertically and another ball Q is thrown horizontally from the  same height and at the same time. If air resistance is neglected, then 

1. Ball P reaches the ground first

2. Ball Q reaches the ground first

3. Both reach the ground at the same time

4. The respective masses of the two balls will decide the time