A particle is moving along x-axis. The velocity v of particle varies with its position x as $\mathrm{v}=\frac{1}{\mathrm{x}}$. Find velocity of particle as a function of time t given that at t=0, x=1 .

1.  $\mathrm{v}=\sqrt{2\mathrm{t}+1}$

2.  $\mathrm{v}=\frac{1}{\sqrt{2\mathrm{t}+1}}$

3.  $\mathrm{v}=\frac{1}{\mathrm{t}}$

4.  None of these

A motor boat of mass m moving along a lake with velocity ${\mathrm{V}}_0$. At t=0, the engine of the boat is shut down. Magnitude of resistance force offered to the boat is equal to rV. (V is instantaneous speed). What is the total distance covered till it stops completely? $\left[\mathrm{Hint}:<mspace\; width="1em"></mspace>\mathrm{F}\left(\mathrm{x}\right)=\mathrm{mV}\frac{\mathrm{dV}}{\mathrm{dx}}=-\mathrm{rV}\right]$

(1)  ${\mathrm{mV}}_0/\mathrm{r}$

(2)  $3<mspace\; width="1em"></mspace>{\mathrm{mV}}_0/2\mathrm{r}$

(3)  ${\mathrm{mV}}_0/2\mathrm{r}$

(4)  $2{\mathrm{mV}}_0/\mathrm{r}$

If a curve is governed by the equation y = sinx, then the area enclosed by the curve and x-axis between x = 0 and x =$\mathrm{\pi }$ is (shaded region):
           
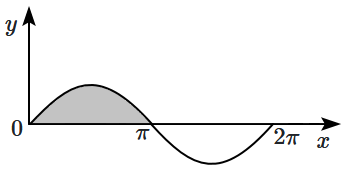
1. \(1\) unit
2. \(2\) units
3. \(3\) units
4. \(4\) units

The acceleration of a particle starting from rest varies with time according to relation, $a=\alpha <mspace\; width="1em"></mspace>t+\beta$. The velocity of the particle at time instant \(t\) is: \(\left(\text{Here,}~ a=\frac{dv}{dt}\right)\)

1. $\alpha t^2+\beta t$

2. $\alpha t^2+\frac{\beta t}{2}$

3. $\frac{\alpha t^2}{2}+\beta t$

4. $2\alpha t^2+\beta t$

The displacement of the particle is zero at \(t=0\) and at \(t=t\) it is \(x\). It starts moving in the \(x\)-direction with a velocity that varies as \(v = k \sqrt{x}\), where \(k\) is constant. The velocity will: (Here, \(v=\frac{dx}{dt}\))

The acceleration of a particle is given as \(a= 3x^2\).  At \(t=0,v=0\) and \(x=0\). It can then be concluded that the velocity at \(t=2~\text{s}\) will be: (Here, \(a=v\frac{dv}{dx}\))
1. \(0.05~\text{m/s}\)
2. \(0.5~\text{m/s}\)
3. \(5~\text{m/s}\)
4. \(50~\text{m/s}\)

The acceleration of a particle is given by \(a=3t\) at \(t=0\), \(v=0\), \(x=0\). The velocity and displacement at \(t = 2~\text{sec}\) will be:
\(\left(\text{Here,} ~a=\frac{dv}{dt}~ \text{and}~v=\frac{dx}{dt}\right)\)
1. \(6~\text{m/s}, 4~\text{m}\)
2. \(4~\text{m/s}, 6~\text{m}\)
3. \(3~\text{m/s}, 2~\text{m}\)
4. \(2~\text{m/s}, 3~\text{m}\)

If the acceleration \(a(t)= 4t+6\), the velocity of a particle starting from rest is: \(\left(\text{here} ,  a = \frac{d v}{d t}\right)\)
1. \(2t+6\)
2. \(4\)
3. \(0\)
4. \(2t^2+6t\)

A force of $F\left(x\right)=2x^2+3$ N is applied to an object. How much work is done, in Joules, moving the object from x=1 to x=4 meters? $\left(work={\int }_a^{b}F\left(x\right)<mspace\; width="1em"></mspace>dx\right)$

1. $\frac{11}{3}<mspace\; width="1em"></mspace>J$

2. 51 J

3. $\frac{5}{3}<mspace\; width="1em"></mspace>J$

4. $\frac{164}{3}<mspace\; width="1em"></mspace>J$

A car has a certain displacement between 0 seconds and 2 seconds. If we defined its velocity as v(t)=6t-5, then the displacement in meters is: $\left(\mathrm{Here},<mspace\; width="1em"></mspace>\mathrm{v}=\frac{\mathrm{ds}}{\mathrm{dt}}\right)$

1. 1 m

2. 2 m

3. 3 m

4. 4 m