The circumference of the Bohr orbit for the H atom is related to the de Broglie wavelength associated with the electron revolving around the orbit by the following relation: 
1. $2\mathrm{\pi r}=\mathrm{n\lambda }$
2. $\mathrm{\pi r}$ $=$ $2\mathrm{n\lambda }$
3. $\mathrm{mvr}$ $=$ $\mathrm{n\lambda }$
4. $\mathrm{vr}$ $=$ $2\mathrm{n\lambda }$

 The largest de Broglie wavelength among the following (all have equal velocity) is: 

1.  ${\mathrm{CO}}_2$ molecule

2.  ${\mathrm{NH}}_3$ molecule

3.  Electron

4.  Proton

The wavelength of an electron moving with a velocity of 2.05 × 10⁷ m s^–1  would be:  

\(1 .\) \(4 . 65\) \(\times\) \(10^{- 12}\) \(m\)

\(2 .\) \(3 . 55\) \(\times\) \(10^{-11}\) \(m\)

\(3 .\) \(2 . 34\) \(\times\) \(10^{11}\) \(m\)

\(4 .\) \(6 . 43\) \(\times\) \(10^{ -11}\) \(m\)

If the velocity of the electron is 1.6 × 10⁶ ${\mathrm{ms}}^{-1}$. The de Broglie wavelength associated with this electron is:  

$1.$ $590$ $\mathrm{pm}$
$2.$ $455$ $\mathrm{pm}$
$3.$ $512$ $\mathrm{pm}$
$4.$ $401$ $\mathrm{pm}$

Identify the graph that correctly depicts the variation of momentum with the de-Broglie wavelength of a particle. 

1.		2.
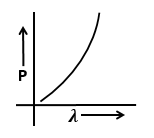3.		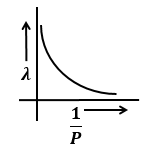4.

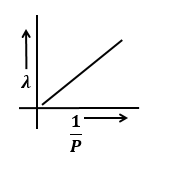Incorrect statement among the following is: 

The velocity associated with a proton moving at a potential difference of 1000 V is 4.37 × 10⁵ ms^–1. If the hockey ball of mass 0.1 kg is moving with this velocity, then the wavelength associated with this velocity would be:

$1.$ $1.52$ $\times {10}^{-38}$ $\mathrm{m}$
$2.$ $2.54$ $\times$ ${10}^{-32}$ $\mathrm{m}$
$3.$ $1.52$ $\times$ ${10}^{-36}$ $\mathrm{m}$
$4.$ $3.19$ $\times$ ${10}^{-34}$ $\mathrm{m}$

The kinetic energy of an electron is \(3.0 \times 10^{-25}~ \mathrm J.\) Its wave length would be: 
1. \(8.96 \times 10^{-7}~ \mathrm m\)
2. \(4.37 \times 10^{-6}~ \mathrm m\)
3. \(1.32 \times 10^{-7}~ \mathrm m\)
4. \(2.89 \times 10^{-4}~ \mathrm m\)

What is the velocity associated with a neutron that has a wavelength of 800 pm?