- 1(current)
Q. No.A particle \((P)\) of mass \(m\) is placed on the axis of a uniform circular ring of radius \(R\) and mass \(M.\) Its distance \((OP)\) from the centre \((O)\) of the ring is equal to \(R.\) Let the net gravitational field at the centre of the ring be \(g.\) Then, the gravitational potential energy of the interaction of the system is:
1. \(-MgR\)
2. \(-mgR\)
3. \(\dfrac{-MgR}{\sqrt2}\)
4. \(\dfrac{-mgR}{\sqrt2}\)
1. \(-MgR\)
2. \(-mgR\)
3. \(\dfrac{-MgR}{\sqrt2}\)
4. \(\dfrac{-mgR}{\sqrt2}\)
Subtopic: Electric Potential Energy |
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Match the charge distribution mentioned in Column I with the graph of corresponding potential energy of interaction under Column II.
| Column I Charge distribution |
Column II Interaction energy |
||
| \(\mathrm{(A)}\) |  Two point charges separated by distance \(x\) |
\(\mathrm{(I)}\) |  |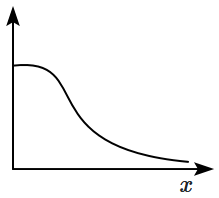
| \(\mathrm{(B)}\) |  Interaction energy of a point charge with a uniformly charged spherical surface |
\(\mathrm{(II)}\) |  |
| \(\mathrm{(C)}\) |  Interaction energy of a point charge with a uniform spherical volume charge |
\(\mathrm{(III)}\) |  |
| \(\mathrm{(D)}\) |  Interaction energy of a dipole & a point charge |
\(\mathrm{(IV)}\) |  |
| 1. | \(\mathrm{A\text-II,B\text-I,C\text-IV,D\text-II}\) |
| 2. | \(\mathrm{A\text-II,B\text-IV,C\text-II,D\text-III}\) |
| 3. | \(\mathrm{A\text-II,B\text-II,C\text-II,D\text-IV}\) |
| 4. | \(\mathrm{A\text-II,B\text-IV,C\text-I,D\text-III}\) |
Subtopic: Electric Potential Energy |
86%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
A uniformly charged metallic sphere holds a total charge \(Q_0\) and has a potential \(V_0.\) The total potential energy stored is:
| 1. | \(Q_0V_0\) | 2. | \(\dfrac{Q_0V_0}{2}\) |
| 3. | \(\dfrac{Q_0V_0}{4}\) | 4. | \(-Q_0V_0\) |
Subtopic: Electric Potential Energy |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Four identical point charges \(q,\) each are fixed at the corners of a square of side \(a.\) The work done in bringing a point charge \(q,\) from infinity and placing it at the centre of the square is: \(\left(k=\dfrac{1}{4\pi\varepsilon_0}\right)\)
1. \(k.\dfrac{4q^2}{a}\)
2. \(k.\dfrac{4\sqrt2q^2}{a}\)
3. \(k.\dfrac{4q^2}{a\sqrt2}\)
4. zero
1. \(k.\dfrac{4q^2}{a}\)
2. \(k.\dfrac{4\sqrt2q^2}{a}\)
3. \(k.\dfrac{4q^2}{a\sqrt2}\)
4. zero
Subtopic: Electric Potential Energy |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
A particle of charge \(q,\) mass \(m\) falls under gravity starting from rest. It falls through a height \(H,\) while being acted upon by an electric field, in addition to gravity. At the end of its motion, it briefly comes to rest. The potential difference between the two extreme points of its motion is:
| 1. | \(\dfrac{mgH}{q}\) | 2. | \(\dfrac{2mgH}{q}\) |
| 3. | \(\dfrac{mgH}{2q}\) | 4. | zero |
Subtopic: Electric Potential Energy |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
A pair of identical point charges (\(q\)-each) are placed at the two vertices of an equilateral triangle. What charge \((Q)\) should be placed at the third vertex, so that the potential energy of the charge distribution is doubled?
| 1. | \(q\) | 2. | \(\Large\frac{q}{2}\) |
| 3. | \(2q\) | 4. | \(4q\) |
Subtopic: Electric Potential Energy |
62%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
A point charge \(q\) is placed at the centre of a uniformly charged ring of radius \(R,\) carrying a charge \(Q. \) The potential energy of interaction between them is: \(\left(k={\Large\frac{1}{4\pi\varepsilon_0}}\right)\)
| 1. | \(k{\Large\frac{qQ}{R}}\) | 2. | \(k{\Large\frac{qQ}{2\pi R}}\) |
| 3. | \(k{\Large\frac{\pi qQ}{R}}\) | 4. | zero |
Subtopic: Electric Potential Energy |
71%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
The work done by electric field in taking a point charge \((q),\) from the centre \((O)\) of a uniformly charged, thin hemispherical shell (charge: \(Q\)) to a point \(A,\) along the path shown in the figure, is: \(\left(k={\Large\frac{1}{4\pi\varepsilon_0}},OA=3R\right)\)
1. zero
2. \(\Large\frac{kqQ}{3R}\)
3. \(\Large\frac{2kqQ}{3R}\)
4. none of the above
1. zero
2. \(\Large\frac{kqQ}{3R}\)
3. \(\Large\frac{2kqQ}{3R}\)
4. none of the above
Subtopic: Electric Potential Energy |
63%
From NCERT
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
Hints
To view explanation, please take trial in the course.
NEET 2026 - Target Batch - Vital
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.