Q. No.The net resistance of the circuit between \(A\) and \(B\) is:
| 1. | \(\frac{8}{3}~\Omega\) | 2. | \(\frac{14}{3}~\Omega\) |
| 3. | \(\frac{16}{3}~\Omega\) | 4. | \(\frac{22}{3}~\Omega\) |
| 1. | \(7R\) | 2. | \(5R\) |
| 3. | \(4R\) | 4. | \(3R\) |
In the circuit shown in the figure below, the current supplied by the battery is:
1. \(2\) A
2. \(1\) A
3. \(0.5\) A
4. \(0.4\) A
In a Wheatstone bridge, all four arms have equal resistance \(R.\) If the resistance of the galvanometer arm is also \(R,\) the equivalent resistance of the combination is:
| 1. | \(R/4\) | 2. | \(R/2\) |
| 3. | \(R\) | 4. | \(2R\) |
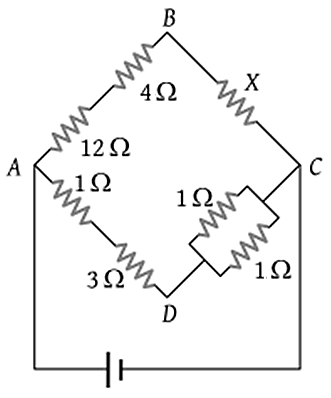
In the circuit shown in the figure below, if the potential difference between \(B\) and \(D\) is zero, then value of the unknown resistance \(X\) is:
| 1. | \(4~\Omega\) | 2. | \(2~\Omega\) |
| 3. | \(3~\Omega\) | 4. | EMF of a cell is required to find the value of \(X\) |
Three resistances \(\mathrm P\), \(\mathrm Q\), and \(\mathrm R\), each of \(2~\Omega\) and an unknown resistance \(\mathrm{S}\) form the four arms of a Wheatstone bridge circuit. When the resistance of \(6~\Omega\) is connected in parallel to \(\mathrm{S}\), the bridge gets balanced. What is the value of \(\mathrm{S}\)?
| 1. | \(2~\Omega\) | 2. | \(3~\Omega\) |
| 3. | \(6~\Omega\) | 4. | \(1~\Omega\) |
Figure \((a)\) below shows a Wheatstone bridge in which \(P,Q,R,S\) are fixed resistances, \(G\) is a galvanometer, and \(B\) is a battery. For this particular case, the galvanometer shows zero deflection. Now, only the positions of \(B\) and \(G\) are interchanged. as shown in figure \((b).\) The new deflection of the galvanometer:
| 1. | is to the left |
| 2. | is to the right |
| 3. | is zero |
| 4. | depends on the values of \(P,Q,R,S\) |
2. \(0.1~\text{A}\)
3. \(2.0~\text{A}\)
4. \(1.0~\text{A}\)
| Column I | Column II | ||
| (A) | Equivalent resistance between \(a\) and \(b\) | (P) | \(\dfrac{R}{2}\) |
| (B) | Equivalent resistance between \(a\) and \(c\) | (Q) | \(\dfrac{5R}{8}\) |
| (C) | Equivalent resistance between \(b\) and \(d\) | (R) | \(R\) |
| 1. | A → P, B → Q, C → R |
| 2. | A → Q, B → P, C → R |
| 3. | A → R, B → P, C → Q |
| 4. | A → R, B → Q, C → P |
For the network shown in the figure below, the value of the current \(i\) is:
1. \(\frac{18V}{5}\)
2. \(\frac{5V}{9}\)
3. \(\frac{9V}{35}\)
4. \(\frac{5V}{18}\)
© 2024 GoodEd Technologies Pvt. Ltd.