A \(5~\text A\) fuse wire can withstand a maximum power of \(1~\text W\) in a circuit. The resistance of the fuse wire is:
1. \(5~\Omega\)
2. \(0.04~\Omega\)
3. \(0.2~\Omega\)
4. \(0.4~\Omega\)
The total power dissipated in watts in the circuit shown below is:


| 1. | \(16\) W | 2. | \(40\) W |
| 3. | \(54\) W | 4. | \(4\) W |
If the voltage across a bulb rated \((220~\text{V}\text-100~\text{W})\) drops by \(2.5\%\) of its rated value, the percentage of the rated value by which the power would decrease is:
1. \(20\%\)
2. \(2.5\%\)
3. \(5\%\)
4. \(10\%\)
Power consumed in the given circuit is \(P_1.\) On interchanging the position of \(3~\Omega\) and \(12~\Omega\) resistances, the new power consumption is \(P_2.\) The ratio of \(\dfrac{P_2}{P_1}\) is:
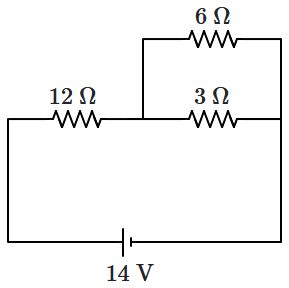
| 1. | \(2\) | 2. | \(\dfrac 12\) |
| 3. | \(\dfrac 35\) | 4. | \(\dfrac 25\) |
For the given circuit, the value of the resistance in which the maximum heat is produced is:
1. \(2~\Omega\)
2. \(6~\Omega\)
3. \(4~\Omega\)
4. \(12~\Omega\)
| 1. | \(\dfrac{a^3R}{3b}\) | 2. | \(\dfrac{a^3R}{2b}\) |
| 3. | \(\dfrac{a^3R}{b}\) | 4. | \(\dfrac{a^3R}{6b}\) |
| 1. | \(10^{\circ}\text{C}\) | 2. | \(5^{\circ}\text{C}\) |
| 3. | \(20^{\circ}\text{C}\) | 4. | \(15^{\circ}\text{C}\) |





