| (A) | The charge stored in it increases. |
| (B) | The energy stored in it decreases. |
| (C) | Its capacitance increases. |
| (D) | The ratio of charge to its potential remains the same. |
| (E) | The product of charge and voltage increases. |
| 1. | (A), (C) and (E) only |
| 2. | (B), (D) and (E) only |
| 3. | (A), (B) and (C) only |
| 4. | (A), (B) and (E) only |
| 1. | \(15\) | 2. | \(7.5\) |
| 3. | \(0.3\) | 4. | \(150\) |

| 1. | \(1.5\times 10^{-6}~\text{J}\) | 2. | \(4.5\times 10^{-6}~\text{J}\) |
| 3. | \(3.25\times 10^{-6}~\text{J}\) | 4. | \(2.25\times 10^{-6}~\text{J}\) |
A parallel plate capacitor has a uniform electric field \(\vec{E}\) in the space between the plates. If the distance between the plates is \(d\) and the area of each plate is \(A\) the energy stored in the capacitor is:
\(\left ( \varepsilon_{0} = \text{permittivity of free space} \right )\)
1. \(\frac{1}{2}\varepsilon_0 E^2 Ad\)
2. \(\frac{E^2 Ad}{\varepsilon_0}\)
3. \(\frac{1}{2}\varepsilon_0 E^2 \)
4. \(\varepsilon_0 EAd\)
Two identical capacitors \(C_{1}\) and \(C_{2}\) of equal capacitance are connected as shown in the circuit. Terminals \(a\) and \(b\) of the key \(k\) are connected to charge capacitor \(C_{1}\) using a battery of emf \(V\) volt. Now disconnecting \(a\) and \(b\) terminals, terminals \(b\) and \(c\) are connected. Due to this, what will be the percentage loss of energy?

| 1. | \(75\%\) | 2. | \(0\%\) |
| 3. | \(50\%\) | 4. | \(25\%\) |
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:
| 1. | decreases by a factor of \(2\) |
| 2. | remains the same |
| 3. | increases by a factor of \(2\) |
| 4. | increases by a factor of \(4\) |
A capacitor of \(2~\mu\text{F}\) is charged as shown in the figure. When the switch \({S}\) is turned to position \(2,\) the percentage of its stored energy dissipated is:
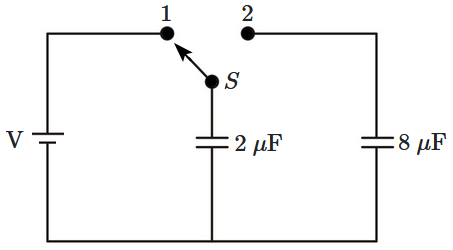
2. \(75\%\)
3. \(80\%\)
4. \(0\%\)
A parallel plate air capacitor of capacitance \(C\) is connected to a cell of emf \(V\) and then disconnected from it. A dielectric slab of dielectric constant \(K,\) which can just fill the air gap of the capacitor is now inserted in it. Which of the following is incorrect?
| 1. | The potential difference between the plates decreases \(K\) times. |
| 2. | The energy stored in the capacitor decreases \(K\) times. |
| 3. | The change in energy stored is \(\frac{1}{2}CV^{2}\left ( \frac{1}{K} -1\right )\) |
| 4. | The charge on the capacitor is not conserved. |
A parallel plate capacitor has a uniform electric field \(E\) in the space between the plates. If the distance between the plates is \(d\) and the area of each plate is \(A,\) the energy stored in the capacitor is:
1. \(\frac{E^2 Ad}{\varepsilon_0}\)
2. \(\frac{1}{2}\varepsilon_0E^2 Ad\)
3. \(\varepsilon_0EAd\)
4. \(\frac{1}{2}\varepsilon_0E^2 \)
A parallel plate condenser has a uniform electric field \(E\)(V/m) in the space between the plates. If the distance between the plates is \(d\)(m) and area of each plate is \(A(\text{m}^2)\), the energy (joule) stored in the condenser is:
| 1. | \(\dfrac{1}{2}\varepsilon_0 E^2\) | 2. | \(\varepsilon_0 EAd\) |
| 3. | \(\dfrac{1}{2}\varepsilon_0 E^2Ad\) | 4. | \(\dfrac{E^2Ad}{\varepsilon_0}\) |




