Given below are two statements:
| Statement I: | If the acceleration of a particle is directed towards a fixed point, and proportional to the distance from that point – the motion is SHM. |
| Statement II: | During SHM, the kinetic energy of the particle oscillates at twice the frequency of the SHM. |
| 1. | Statement I is incorrect and Statement II is correct. |
| 2. | Both Statement I and Statement II are correct. |
| 3. | Both Statement I and Statement II are incorrect. |
| 4. | Statement I is correct and Statement II is incorrect. |
Subtopic: Energy of SHM |
Level 3: 35%-60%
Hints
During simple harmonic motion of a body, the energy at the extreme position is:
| 1. | both kinetic and potential |
| 2. | is always zero |
| 3. | purely kinetic |
| 4. | purely potential |
Subtopic: Energy of SHM |
80%
Level 1: 80%+
NEET - 2022
Hints
The average energy in one time period in simple harmonic motion is:
1. \(\dfrac{1}{2} m \omega^{2} A^{2}\)
2. \(\dfrac{1}{4} m \omega^{2} A^{2}\)
3. \(m \omega^{2} A^{2}\)
4. zero
Subtopic: Energy of SHM |
62%
Level 2: 60%+
Hints
A particle of mass \(m\) is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
| 1. |  |
2. |  |
| 3. | 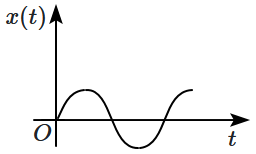 |
4. |  |
Subtopic: Energy of SHM |
Level 3: 35%-60%
AIPMT - 2011
Hints
Match List-I with List-II.
Choose the correct answer from the options given below:
| List-I (\(x \text{-}y\) graphs) |
List-II (Situations) |
||
| (a) |  |
(i) | Total mechanical energy is conserved |
| (b) |  |
(ii) | Bob of a pendulum is oscillating under negligible air friction |
| (c) |  |
(iii) | Restoring force of a spring |
| (d) |  |
(iv) | Bob of a pendulum is oscillating along with air friction |
Choose the correct answer from the options given below:
| (a) | (b) | (c) | (d) | |
| 1. | (iv) | (ii) | (iii) | (i) |
| 2. | (iv) | (iii) | (ii) | (i) |
| 3. | (i) | (iv) | (iii) | (ii) |
| 4. | (iii) | (ii) | (i) | (iv) |
Subtopic: Energy of SHM |
86%
Level 1: 80%+
NEET - 2022
Hints



