Which of the following graph shows the variation of pressure P with volume V for an ideal gas at a constant temperature?

1.		2.
3.		4.

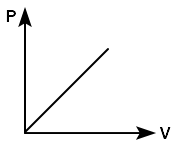
A gas performs the minimum work when it expands:

An ideal gas goes from \(A\) to \(B\) via two processes, \(\mathrm{I}\) and \(\mathrm{II},\) as shown. If \(\Delta U_1\) and \(\Delta U_2\) are the changes in internal energies in processes \(\mathrm{I}\) and \(\mathrm{II},\) respectively,  (\(P:\) pressure, \(V:\) volume) then:

An ideal monoatomic gas \(\left(\gamma = \frac{5}{3}\right )\) absorbs 50 cal in an isochoric process. The increase in internal energy of the gas is:

The pressure-temperature \((P\text-T)\) graph for two processes, \(A\) and \(B,\) in a system is shown in the figure. If \(W_1\) and \(W_2\)${\mathrm{}}_{}$ are work done by the gas in process \(A\) and \(B\) respectively, then:

The variation of molar heat capacity at constant volume ${\mathrm{C}}_{\mathrm{V}}$ with temperature T for a monatomic gas is:

1.		2.
3.		4.

When a system is moved from state \(a\) to state \(b\) along the path \(acb\), it is discovered that the system absorbs \(200~\text{J}\) of heat and performs \(80~\text{J}\) of work.  Along the path \(adb\), heat absorbed \(Q =144~\text{J}\). The work done along the path \(adb\) is:

In the cyclic process shown in the pressure-volume \((P-V)\) diagram, the change in internal energy is equal to:

1. $\pi {\left(\frac{{\mathrm{P}}_2-{\mathrm{P}}_1}{2}\right)}^2$

2. $\mathrm{\pi }{\left(\frac{{\mathrm{V}}_2-{\mathrm{V}}_1}{2}\right)}^2$

3. $\frac{\mathrm{\pi }}{4}({\mathrm{P}}_2-{\mathrm{P}}_1)({\mathrm{V}}_2-{\mathrm{V}}_1)$

4. zero