- 1(current)
Q. No.An ideal gas goes from \(A\) to \(B\) via two processes, \(\mathrm{I}\) and \(\mathrm{II},\) as shown. If \(\Delta U_1\) and \(\Delta U_2\) are the changes in internal energies in processes \(\mathrm{I}\) and \(\mathrm{II},\) respectively, (\(P:\) pressure, \(V:\) volume) then:
| 1. | \(∆U_1 > ∆U_2\) | 2. | \(∆U_1 < ∆U_2\) |
| 3. | \(∆U_1 = ∆U_2\) | 4. | \(∆U_1 \leq ∆U_2\) |
(where symbols have their usual meanings)
1. \(C_P = \frac{\gamma R}{\gamma-1 }\)
2. \(C_P-C_V= R\)
3. \(\Delta U = \frac{P_fV_f-P_iV_i}{1-\gamma}\)
4. \(C_V = \frac{R}{\gamma-1 }\)
If \(n\) moles of an ideal gas is heated at a constant pressure from \(50^\circ\text C\) to \(100^\circ\text C,\) the increase in the internal energy of the gas will be:
\(\left(\frac{C_{p}}{C_{v}} = \gamma\ ~\text{and}~\ R = \text{gas constant}\right)\)
| 1. | \(\dfrac{50nR}{\gamma - 1}\) | 2. | \(\dfrac{100nR}{\gamma - 1}\) |
| 3. | \(\dfrac{50n\gamma R}{\gamma - 1}\) | 4. | \(\dfrac{25n\gamma R}{\gamma - 1}\) |
When an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied which increases the internal energy of the gas is:
| 1. | \(\dfrac{2}{5}\) | 2. | \(\dfrac{3}{5}\) |
| 3. | \(\dfrac{3}{7}\) | 4. | \(\dfrac{5}{7}\) |
Two cylinders contain the same amount of an ideal monoatomic gas. The same amount of heat is given to two cylinders. If the temperature rise in cylinder A is T0, then the temperature rise in cylinder B will be:
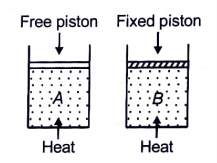
1.
2.
3.
4.
The specific heat of a gas in an isothermal process is:
| 1. | Infinite | 2. | Zero |
| 3. | Negative | 4. | Remains constant |
The volume \((V)\) of a monatomic gas varies with its temperature \((T),\) as shown in the graph. The ratio of work done by the gas to the heat absorbed by it when it undergoes a change from state \(A\) to state \(B\) will be:
| 1. | \(\dfrac{2}{5}\) | 2. | \(\dfrac{2}{3}\) |
| 3. | \(\dfrac{1}{3}\) | 4. | \(\dfrac{2}{7}\) |
- 1(current)
Q. No.
© 2025 GoodEd Technologies Pvt. Ltd.