Consider a cycle followed by an engine (figure).

1 to 2 is isothermal,
2 to 3 is adiabatic,
3 to 1 is adiabatic.
Such a process does not exist, because:
(a)
heat is completely converted to mechanical energy in such a process, which is not possible.
(b)
In this process, mechanical energy is completely converted to heat, which is not possible.
(c)
curves representing two adiabatic processes don’t intersect.
(d)
curves representing an adiabatic process and an isothermal process don't intersect.
Choose the correct alternatives:
1.
(a), (b)
2.
(a), (c)
3.
(b), (c)
4.
(c), (d)

1 to 2 is isothermal,
2 to 3 is adiabatic,
3 to 1 is adiabatic.
Such a process does not exist, because:
The figure shows the \((P\text-V)\) diagram of an ideal gas undergoing a change of state from \(A\) to \(B.\) Four different paths \(\mathrm{I, II, III}\) and \(\mathrm{IV},\) as shown in the figure, may lead to the same change of state.

| (a) | The change in internal energy is the same in cases \(\mathrm{IV}\) and \(\mathrm{III}\) but not in cases \(\mathrm{I}\) and \(\mathrm{II}.\) |
| (b) | The change in internal energy is the same in all four cases. |
| (c) | The work done is maximum in case \(\mathrm{I}.\) |
| (d) | The work done is minimum in case \(\mathrm{II}.\) |
Which of the following options contains only correct statements?
| 1. | (b), (c) and (d) only | 2. | (a) and (d) only |
| 3. | (b) and (c) only | 4. | (a), (c) and (d) only |
The pressure and volume of a gas are changed as shown in the P-V diagram. The temperature of the gas will:
| 1. | increase as it goes from A to B. |
| 2. | increase as it goes from B to C. |
| 3. | remain constant during these changes. |
| 4. | decrease as it goes from D to A. |
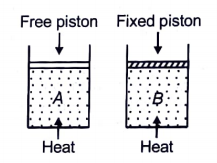
Two cylinders contain the same amount of an ideal monoatomic gas. The same amount of heat is given to two cylinders. If the temperature rise in cylinder A is T0, then the temperature rise in cylinder B will be:
1.
2.
3.
4.
(where symbols have their usual meanings)
1. \(C_P = \frac{\gamma R}{\gamma-1 }\)
2. \(C_P-C_V= R\)
3. \(\Delta U = \frac{P_fV_f-P_iV_i}{1-\gamma}\)
4. \(C_V = \frac{R}{\gamma-1 }\)
| 1. | \(\Delta {U}=-{W}\) in an isothermal process. |
| 2. | \(\Delta {U}={W}\) in an isothermal process. |
| 3. | \(\Delta {U}=-{W}\) in an adiabatic process. |
| 4. | \(\Delta {U}={W}\) in an adiabatic process. |
1. \(0\)
2. \(5~\text{J}\)
3. \(1~\text{J}\)
4. \(3~\text{J}\)
Find out the total heat given to diatomic gas in the process \(A\rightarrow B \rightarrow C\): \(( B\rightarrow C\) is isothermal)

1. \(P_0V_0+ 2P_0V_0\ln 2\)
2. \(\frac{1}{2}P_0V_0+ 2P_0V_0\ln 2\)
3. \(\frac{5}{2}P_0V_0+ 2P_0V_0\ln 2\)
4. \(3P_0V_0+ 2P_0V_0\ln 2\)
\(0.04\) mole of an ideal monatomic gas is allowed to expand adiabatically so that its temperature changes from \(800~\text{K}\) to \(500~\text{K}.\) The work done during expansion is nearly equal to:

| 1. | \(129.6~\text J\) | 2. | \(-129.6~\text J\) |
| 3. | \(149.6~\text J\) | 4. | \(-149.6~\text J\) |

1. \(V_1= V_2\)
2. \(V_1> V_2\)
3. \(V_1< V_2\)
4. \(V_1\ge V_2\)







