The incorrect relation is:
(where symbols have their usual meanings)
1. \(C_P = \frac{\gamma R}{\gamma-1 }\)
2. \(C_P-C_V= R\)
3. \(\Delta U = \frac{P_fV_f-P_iV_i}{1-\gamma}\)
4. \(C_V = \frac{R}{\gamma-1 }\)
Two cylinders contain the same amount of an ideal monoatomic gas. The same amount of heat is given to two cylinders. If the temperature rise in cylinder A is T0, then the temperature rise in cylinder B will be:
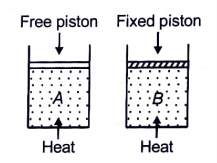
1.
2.
3.
4.
The pressure and volume of a gas are changed as shown in the P-V diagram. The temperature of the gas will:
| 1. | increase as it goes from A to B. |
| 2. | increase as it goes from B to C. |
| 3. | remain constant during these changes. |
| 4. | decrease as it goes from D to A. |
The figure shows the \((P\text-V)\) diagram of an ideal gas undergoing a change of state from \(A\) to \(B.\) Four different paths \(\mathrm{I, II, III}\) and \(\mathrm{IV},\) as shown in the figure, may lead to the same change of state.

| (a) | The change in internal energy is the same in cases \(\mathrm{IV}\) and \(\mathrm{III}\) but not in cases \(\mathrm{I}\) and \(\mathrm{II}.\) |
| (b) | The change in internal energy is the same in all four cases. |
| (c) | The work done is maximum in case \(\mathrm{I}.\) |
| (d) | The work done is minimum in case \(\mathrm{II}.\) |
Which of the following options contains only correct statements?
| 1. | (b), (c) and (d) only | 2. | (a) and (d) only |
| 3. | (b) and (c) only | 4. | (a), (c) and (d) only |
Consider a cycle followed by an engine (figure).
1 to 2 is isothermal,
2 to 3 is adiabatic,
3 to 1 is adiabatic.
Such a process does not exist, because:
| (a) | heat is completely converted to mechanical energy in such a process, which is not possible. |
| (b) | In this process, mechanical energy is completely converted to heat, which is not possible. |
| (c) | curves representing two adiabatic processes don’t intersect. |
| (d) | curves representing an adiabatic process and an isothermal process don't intersect. |
Choose the correct alternatives:
| 1. | (a), (b) | 2. | (a), (c) |
| 3. | (b), (c) | 4. | (c), (d) |
1. \(0\)
2. \(5~\text{J}\)
3. \(1~\text{J}\)
4. \(3~\text{J}\)
Find out the total heat given to diatomic gas in the process \(A\rightarrow B \rightarrow C\): \(( B\rightarrow C\) is isothermal)

1. \(P_0V_0+ 2P_0V_0\ln 2\)
2. \(\frac{1}{2}P_0V_0+ 2P_0V_0\ln 2\)
3. \(\frac{5}{2}P_0V_0+ 2P_0V_0\ln 2\)
4. \(3P_0V_0+ 2P_0V_0\ln 2\)
| 1. | \(\Delta {U}=-{W}\) in an isothermal process. |
| 2. | \(\Delta {U}={W}\) in an isothermal process. |
| 3. | \(\Delta {U}=-{W}\) in an adiabatic process. |
| 4. | \(\Delta {U}={W}\) in an adiabatic process. |
\(0.04\) mole of an ideal monatomic gas is allowed to expand adiabatically so that its temperature changes from \(800~\text{K}\) to \(500~\text{K}.\) The work done during expansion is nearly equal to:

| 1. | \(129.6~\text J\) | 2. | \(-129.6~\text J\) |
| 3. | \(149.6~\text J\) | 4. | \(-149.6~\text J\) |

1. \(V_1= V_2\)
2. \(V_1> V_2\)
3. \(V_1< V_2\)
4. \(V_1\ge V_2\)








