A copper rod of \(88\) cm and an aluminium rod of an unknown length have an equal increase in their lengths independent of an increase in temperature. The length of the aluminium rod is:
\(\left(\alpha_{Cu}= 1.7\times10^{-5}~\text{K}^{-1}~\text{and}~\alpha_{Al}= 2.2\times10^{-5}~\text{K}^{-1}\right)\)
1. \(68~\text{cm}\)
2. \(6.8~\text{cm}\)
3. \(113.9~\text{cm}\)
4. \(88~\text{cm}\)

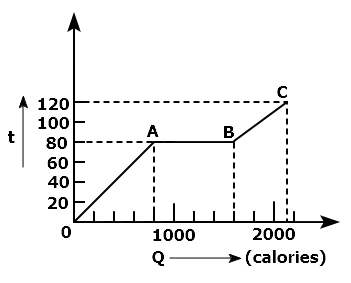
A substance is in solid form at \(0^{\circ}\mathrm{C}\). The amount of heat added to this substance and its temperature are plotted in the following graph. If the relative specific heat capacity of the solid substance is 0.5, from the graph, the specific latent heat of the melting process is: (Specific heat capacity of water = 1000 cal kg^-1 K^-1 )

On a new scale of temperature, which is linear and called the \(\text{W}\) scale, the freezing and boiling points of water are \(39^\circ ~\text{W}\) and \(239^\circ ~\text{W}\) respectively. What will be the temperature on the new scale corresponding to a temperature of \(39^\circ ~\text{C}\) on the Celsius scale?
1. \(78^\circ ~\text{W}\)
2. \(117^\circ ~\text{W}\)
3. \(200^\circ ~\text{W}\)
4. \(139^\circ ~\text{W}\)

The temperature of a body on the Kelvin scale is found to be \(x^\circ~\text K.\) When it is measured by a Fahrenheit thermometer, it is found to be \(x^\circ~\text F,\) then the value of \(x\) is:
1. \(40\)
2. \(313\)
3. \(574.25\)
4. \(301.25\)

Liquid oxygen at \(50~\text K\) is heated up to \(300~\text K\) at a constant pressure of \(1~\text{atm}.\) The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?

1.		2.
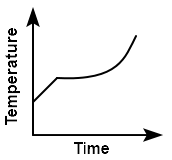3.		4.

If the radius of a star is \(R\) and it acts as a black body, what would be the temperature of the star at which the rate of energy production is \(Q?\)
\(\left(\sigma~ \text{is Stefan-Boltzmann constant}\right)\)
1. \(\dfrac{Q}{4\pi R^2\sigma}\)

2. \(\left(\dfrac{Q}{4\pi R^2\sigma}\right )^{\dfrac{-1}{2}}\)

3. \(\left(\dfrac{4\pi R^2 Q}{\sigma}\right )^{\dfrac{1}{4}}\)

4. \(\left(\dfrac{Q}{4\pi R^2 \sigma}\right)^{\dfrac{1}{4}}\)

Two rods, one made of aluminium and the other made of steel, having initial lengths \(l_1\) and \(l_2\) are connected together to form a single rod of length $l_1+l_2$. The coefficient of linear expansion for aluminium and steel are ${\alpha }_a$ and ${\alpha }_s$ respectively. If the length of each rod increases by the same amount when their temperature is raised by \(t^\circ \mathrm{C},\) then the ratio \(\frac{l_1}{l_1+l_2}\) is:
1. $\frac{{\alpha }_s}{{\alpha }_a}$

2. $\frac{{\alpha }_a}{{\alpha }_s}$

3. $\frac{{\alpha }_a}{{\alpha }_a+{\alpha }_s}$

4. $\frac{{\alpha }_s}{{\alpha }_a+{\alpha }_s}$

Three rods made of the same material and having the same cross-section have been joined as shown in the figure. Each rod has the same length. The left and right ends are kept at \(0^{\circ}\text{C}~\text{and}~90^{\circ}\text{C},\) respectively. The temperature at the junction of the three rods will be:

           
1. \(45^{\circ}\text{C}\)
2. \(60^{\circ}\text{C}\)
3. \(30^{\circ}\text{C}\)
4. \(20^{\circ}\text{C}\)

A block of metal is heated to a temperature much higher than the room temperature and allowed to cool in a room free from air currents. Which of the following curves correctly represents the rate of cooling?

1.		2.
3.		4.

If the sun’s surface radiates heat at \(6.3\times 10^{7}~\text{Wm}^{-2}\) ${\mathrm{}}^{}$then the temperature of the sun, assuming it to be a black body, will be:
\(\left(\sigma = 5.7\times 10^{-8}~\text{Wm}^{-2}\text{K}^{-4}\right)\)
1. \(5.8\times 10^{3}~\text{K}\)
2. \(8.5\times 10^{3}~\text{K}\)
3. \(3.5\times 10^{8}~\text{K}\)
4. \(5.3\times 10^{8}~\text{K}\)