The graph between \(E\) and \(v\) is:
1.

2.

3.
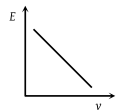
4.





A body moves from rest with a constant acceleration. Which one of the following graphs represents the variation of its kinetic energy K with the distance travelled x ?
1.
2.
3.
4.
The diagrams represent the potential energy U as a function of the inter-atomic distance r. Which diagram corresponds to stable molecules found in nature.
1.
2.
3.
4.
The relationship between the force \(F\) and the position \(x\) of a body is as shown in the figure. The work done in displacing the body from \(x = 1\text{ m}\) to \(x = 5\text{ m}\) will be:
1. \(30\text{ J}\)
2. \(15\text{ J}\)
3. \(25\text{ J}\)
4. \(20\text{ J}\)
A particle is placed at the origin and a force F = kx is acting on it (where k is positive constant). If U(0) = 0, the graph of U(x) versus x will be (where U is the potential energy function)
1.
2.
3.
4.
A spring of force constant k is cut into lengths of ratio 1:2:3. They are connected in series and the new force constant is . If they are connected in parallel and force constant is is
1. 1:6
2. 1:9
3. 1:11
4. 6:11
Consider a drop of rain water having mass \(1\) g falling from a height of \(1\) km. It hits the ground with a speed of \(50\) m/s. Take \(g\) constant with a value of \(10\) m/. The work done by the
(i) gravitational force and the (ii) resistive force of air is:
| 1. | \((i)-10~\text{J}, (ii)-8.25~\text{J}\) |
| 2. | \((i)~1.25~\text{J}, (ii)-8.25~\text{J}\) |
| 3. | \((i)~100~\text{J}, (ii)~8.75~\text{J}\) |
| 4. | \((i)~10~\text{J}, (ii)-8.75~\text{J}\) |
Two identical balls \(\mathrm{A}\) and \(\mathrm{B}\) having velocities of \(0.5~\text{m/s}\) and \(-0.3~\text{m/s}\) respectively collide elastically in one dimension. The velocities of \(\mathrm{B}\) and \(\mathrm{A}\) after the collision respectively will be:
1. \(-0.5 ~\text{m/s}~\text{and}~0.3~\text{m/s}\)
2. \(0.5 ~\text{m/s}~\text{and}~-0.3~\text{m/s}\)
3. \(-0.3 ~\text{m/s}~\text{and}~0.5~\text{m/s}\)
4. \(0.3 ~\text{m/s}~\text{and}~0.5~\text{m/s}\)
1. \(8~\text{J}\)
2. \(11~\text{J}\)
3. \(5~\text{J}\)
4. \(2~\text{J}\)
A body of mass 1 kg begins to move under the action of a time dependent force \(F = 2 t\) \(\hat{i} + 3 t^{2}\ \hat{j}\) N, where \(\hat{i}\) and \(\hat{j}\) are unit vectors along X and Y axis, What power will be developed by the force at the time (t) ?
1. \(\left(2 t^{2} + 4 t^{4}\right) W\)
2. \(\left(2 t^{3} + 3 t^{4}\right) W\)
3. \(\left(2 t^{3} + 3 t^{5}\right) W\)
4. \(\left(2 t + 3 t^{3}\right) W\)



















