Two simple pendulums have time periods T and $\frac{5T}{4}$. They start vibrating at the same instant from the mean position in the same phase. The phase difference between them when bigger pendulum completes one oscillation will be:

1. $\frac{\mathrm{\pi }}{6}$

2. $\frac{\mathrm{\pi }}{4}$

3. $\frac{\mathrm{\pi }}{3}$

4. $\frac{\mathrm{\pi }}{2}$

A simple pendulum is oscillating without damping. When the displacement of the bob is less than maximum, its acceleration vector \(\vec a\) is correctly shown in: 

1.		2.
3.		4.

There is a simple pendulum hanging from the ceiling of a lift. When the lift is stand still, the time period of the pendulum is T. If the resultant acceleration becomes g/4, then the new time period of the pendulum is 

1. 0.8 T

2. 0.25 T

3. 2 T

4. 4 T

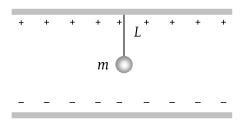
A small sphere carrying a charge ‘q’ is hanging in between two parallel plates by a string of length L. Time period of pendulum is T₀. When parallel plates are charged, the electric field between the plates is E and time period changes to T. The ratio T/T₀ is equal to 

(1) ${\left(\frac{{\displaystyle g+\frac{{\displaystyle qE}}{{\displaystyle m}}}}{{\displaystyle g}}\right)}^{1/2}$           (2) ${\left(\frac{{\displaystyle g}}{{\displaystyle g+\frac{{\displaystyle qE}}{{\displaystyle m}}}}\right)}^{3/2}$

(3) ${\left(\frac{{\displaystyle g}}{{\displaystyle g+\frac{{\displaystyle qE}}{{\displaystyle m}}}}\right)}^{1/2}$           (4) None of these 

The uniform stick of mass m length \(\text L\) is pivoted at the centre. In the equilibrium position shown in the figure, the identical light springs have their natural length. If the stick is turned through a small angle $\theta$, it executes SHM. The frequency of the motion is:

1. \(\frac{1}{2 \pi} \sqrt{\frac{6 K}{m}} \)

2. \(\frac{1}{2 \pi} \sqrt{\frac{3 K}{2 m}} \)

3. \(\frac{1}{2 \pi} \sqrt{\frac{3 K}{m}} \)

4. None of these

A particle undergoes SHM with a time period of 2 seconds. In how much time will it travel from its mean position to a displacement equal to half of its amplitude?

1. $\frac{1}{2}s$

2. $\frac{1}{6}s$

3. $\frac{1}{4}s$

4. $\frac{1}{3}s$

Which of the following figure represents damped harmonic motion?

(i)
(ii)
(iii)
(iv)

1. (i) and (ii)

2. (iii) and (iv)

3. (i), (ii), (iii), and (iv)

4. (i) and  (iv)