A particle is rotating under the central force, in which one of the following quantities is constant:

1.  torque

2.  angular momentum

3.  linear momentum

4.  none of these

A small object of uniform density rolls up a curved surface with an initial velocity \(v.\) It is reached upto a maximum height of \(\frac{3v^{2}}{4g}\) with respect to the initial position. The object is:

1. ring
2. solid sphere
3. hollow sphere
4. disc

A point is at (x, y, z). What is its moment of inertia about x-axis:

1.  $\mathrm{m}\left({\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2\right)$

2.  $\mathrm{m}\left({\mathrm{x}}^2+{\mathrm{y}}^2\right)$

3.  $\mathrm{m}\left({\mathrm{y}}^2+{\mathrm{z}}^2\right)$

4.  $\mathrm{m}\left({\mathrm{x}}^2+{\mathrm{z}}^2\right)$

The disc is placed on the rough horizontal surface given only angular velocity ${\omega }_0$. The velocity of the centre of mass when it starts pure rolling is:

1.  $\frac{{\omega }_{0}R}{2}$

2.  $\frac{{\omega }_{0}R}{3}$

3.  $\frac{{\omega }_{0}R}{4}$

4.  $\frac{{\omega }_{0}R}{6}$

A force 2N is along line y = 3x + 4. The torque about the origin is:

1.  $\frac{5}{\sqrt{10}}\mathrm{Nm}$

2.  $\frac{7}{\sqrt{10}}\mathrm{Nm}$

3.  $\frac{6}{\sqrt{10}}\mathrm{Nm}$

4.  $\frac{8}{\sqrt{10}}\mathrm{Nm}$

A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two-point
masses m and 2m moving in the same horizontal plane with speeds 2v and v
respectively strike the bar as shown below in the figure and stick to the bar after the collision. Denoting angular velocity about the center of mass, total energy, and center of mass velocity of $\omega$, E and ${\mathrm{v}}_{\mathrm{c}}$ respectively, we have after collision

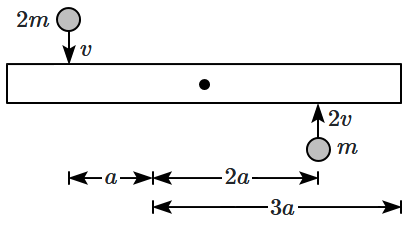
1.  ${\mathrm{v}}_{\mathrm{c}} = 2 \mathrm{m}/\mathrm{s}$

2.  $\mathrm{\omega } = \frac{3}{5}\frac{\mathrm{v}}{\mathrm{a}}$

3.  $\mathrm{\omega } = \frac{\mathrm{v}}{5\mathrm{a}}$

4.  $\mathrm{E} = \frac{2}{3} {\mathrm{mv}}^2$

A uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The ratio of inertia of the loop about
x-axis to that about y-axis is:

1.  >1

2.  <1

3.  =1

4.  =1/2

Four spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then the moment of inertia of the system about an axis about one of the sides of the square is

1. $M{a}^2+2M{b}^2$

2. $M{a}^2$

3. $M{a}^2+4M{b}^2$

4. $\frac{8}{5}M{a}^2+2M{b}^2$

A body of mass m slides down an incline and reaches the bottom with a velocity v. If the same mass were in the form of a ring which rolls down this incline, the velocity of the ring at bottom would have been

1. v

2. $\sqrt{2} v$

3. $\left(1/\sqrt{2}\right)v$

4. $\left(\sqrt{2/5}\right)v$

 
1. \(\frac{3g}{2L}\)
2. \(\frac{3g}{\sqrt{2}L}\)
3. \(\frac{3g}{2\sqrt{2}L}\)
4. \(\frac{6g}{\sqrt{2}L}\)