A solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity v m/s. If sphere climbs up to height h then value of v should be -

                             

1. $\ge \sqrt{\frac{10}{7}\mathrm{gh}}$                                                   

2. $\ge \sqrt{2\mathrm{gh}}$

3. $2\mathrm{gh}$                                                             

4. $\frac{10}{7}\mathrm{gh}$

A projectile is fired at angle $\mathrm{\theta }$ with horizontal with initial speed u. If it breaks into two halves such that one half retraces its path, then the distance of hitting point of the other half from starting point is

1. $\frac{{\mathrm{u}}^2\sin 2\mathrm{\theta }}{\mathrm{g}}$

2. $\frac{2{\mathrm{u}}^2\sin 2\mathrm{\theta }}{\mathrm{g}}$

3. $\frac{{\mathrm{u}}^2\sin 2\mathrm{\theta }}{2\mathrm{g}}$

4. $\frac{{\mathrm{u}}^2\mathrm{sin\theta }}{2\mathrm{g}}$

The value of M, as shown, for which the rod will be in equilibrium is (rod is massless)

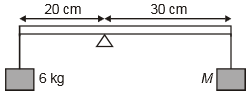
1.  1 kg

2.  2 kg

3.  4 kg

4.  6 kg

The minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination 45$°$ is

1.  2/7

2.  1/3

3.  1/2

4.  2/5

A wheel is rolling along a horizontal ground with a speed o 10 m/s. The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is equal to

1. $2\sqrt{10} m/s$

2. 10 m/s

3. $\sqrt{10} m/s$

4. $10\sqrt{2} m/s$

$\mathrm{A} \mathrm{body} \mathrm{of} \mathrm{mass} \mathrm{m} \mathrm{is} \mathrm{projected} \mathrm{at} \mathrm{a} \mathrm{velocity} {\mathrm{v}}_0$
$\mathrm{with} \mathrm{an} \mathrm{angle} \mathrm{of} \mathrm{projection} \mathrm{\theta }. \mathrm{Angular} \mathrm{momentum}$
$\mathrm{L} \mathrm{of} \mathrm{body} \mathrm{after} \mathrm{time} \mathrm{t} \mathrm{w}.\mathrm{r}.\mathrm{to} \mathrm{origin} \mathrm{is} \mathrm{proportional} \mathrm{to}:$
$1. \mathrm{L}\propto \mathrm{t} 2. \mathrm{L}\propto {\mathrm{t}}^2$
$3. \mathrm{L}\propto {\mathrm{t}}^0 4. \mathrm{L}\propto \sqrt{\mathrm{t}}$

A mass M is moving with constant velocity parallel to the X-axis. Its angular momentum with respect to origin is:

1.  Zero

2.  Remains constant

3.  goes on increasing

4.  goes on decreasing

If I is the moment of inertia of a solid sphere about an axis parallel to diameter of a shpere and at a distance x from it. Which of the following graph represents the variation of I with X?

1.		2.
3.		4.

A particle is rotating under the central force, in which one of the following quantities is constant:

1.  torque

2.  angular momentum

3.  linear momentum

4.  none of these

A small object of uniform density rolls up a curved surface with an initial velocity \(v.\) It is reached upto a maximum height of \(\frac{3v^{2}}{4g}\) with respect to the initial position. The object is:

1. ring
2. solid sphere
3. hollow sphere
4. disc