A wire of length \(L\) meters carrying a current of \(I\) ampere is bent in the form of a circle. What is its magnetic moment?
1. \( \dfrac{{IL}^2}{4} ~\text{A}\text-\text{m}^2 \)
2. \( \dfrac{{I} \times \pi {L}^2}{4} ~\text{A}\text-\text{m}^2 \)
3. \( \dfrac{2 {IL}^2}{\pi}~\text{A}\text-\text{m}^2 \)
4. \( \dfrac{{IL}^2}{4 \pi}~\text{A}\text-\text{m}^2 \)

A straight wire of mass \(200~\text{g}\) and length \(1.5~\text{m}\) carries a current of \(2~\text{A}.\) It is suspended in mid-air by a uniform horizontal magnetic field \(B\) (shown in the figure). What is the magnitude of the magnetic field?

In a region of space, magnetic field is parallel to the positive \(y\text-\)axis and the charged particle is moving along the positive \(x\text-\)axis (as shown in the figure). The directions of Lorentz force for an electron (negative charge) and proton (positive charge) are respectively:

The radius of the path of an electron and frequency (mass $9\times {10}^{-31}<mspace\; width="1em"></mspace>\mathrm{kg}$ and charge $1.6\times {10}^{-19}<mspace\; width="1em"></mspace>\mathrm{C}$) moving at a speed of \(3\times10^7\) m/s in a magnetic field of \(6\times10^{-4}\) T perpendicular to it are respectively:
1. \(24\) cm, \(4\) MHz
2. \(22\) cm, \(4\) MHz
3. \(28\) cm, \(2\) MHz
4. \(26\) cm, \(2\) MHz

An electron $\left(mass<mspace\; width="1em"></mspace>9\times {10}^{-31}<mspace\; width="1em"></mspace>kg<mspace\; width="1em"></mspace>and<mspace\; width="1em"></mspace>charge<mspace\; width="1em"></mspace>1.6\times {10}^{-19}<mspace\; width="1em"></mspace>C\right)$ is moving at a speed of 3 ×10⁷ m/s in a magnetic field perpendicular to it. The energy of the electron in keV is: ( 1 eV = 1.6 × 10^–19 J)

1. 2.5 keV

2. 3.5 keV

3. 20 keV

4. 3.0 keV

A cyclotron’s oscillator frequency is 10 MHz. The radius of its ‘dees’ is 60 cm, what should be the operating magnetic field for accelerating protons and the kinetic energy (in MeV) of the proton beam produced by the accelerator?

1. 0.66 T, 6 MeV

2. 0.33 T, 6 MeV

3. 0.66 T, 7 MeV

4. 0.33 T, 7 MeV

An element \(\Delta l=\Delta x \hat{i}\) is placed at the origin and carries a large current of \(I=10~\text A\) (as shown in the figure). What is the magnetic field on the \(y\text-\)axis at a distance of \(0.5~\text m?\) 
\((\text{Given}~\Delta x=1~\text{cm})\)

Consider a tightly wound \(100\) turn coil of radius \(10\) cm, carrying a current of \(1\) A. What is the magnitude of the magnetic field at the centre of the coil?

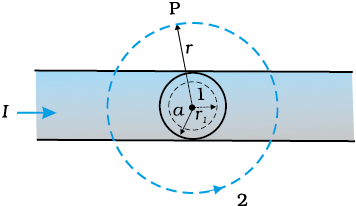
The figure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. If the magnetic field in the region (r < a) is $B_1$ and for (r > a) is $B_2$, then $\frac{B_1}{B_2}$ is:

$1.<mspace\; width="1em"></mspace>\frac{a}{r}$
$2.<mspace\; width="1em"></mspace>\frac{a^2}{r^2}$
$3.<mspace\; width="1em"></mspace>\frac{r^2}{a^2}$
$4.<mspace\; width="1em"></mspace>\frac{r}{a}$