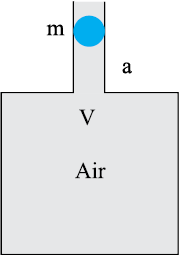
An air chamber of volume V has a neck area of cross-section 'a' into which a ball of mass 'm' just fits and can move up and down without any friction (as shown in the figure). When the ball is pressed down a little and released, it executes SHM. The time period of oscillations is:
(assuming pressure-volume variations of air to be isothermal)
1. \(\mathrm{T}=\frac{1}{2 \pi} \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^3}}\)
2. \(\mathrm{T}=\pi \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^2}}\)
3. \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^2}}\)
4. \(\mathrm{T}=3 \pi \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^2}}\)

1. \(\mathrm{T}=\frac{1}{2 \pi} \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^3}}\)
2. \(\mathrm{T}=\pi \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^2}}\)
3. \(\mathrm{T}=2 \pi \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^2}}\)
4. \(\mathrm{T}=3 \pi \sqrt{\frac{\mathrm{Vm}_{\mathrm{m}}}{\mathrm{Ba}^2}}\)
A circular disc of mass 10 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5 sec. The radius of the disc is 15 cm. The torsional spring constant of the wire is:
1. 2.1 Nm rad−1
2. 0.6 Nm rad−1
3. 3.2 Nm rad−1
4. 1.9 Nm rad−1
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 sec. What is the acceleration of the body when the displacement is 5 cm?
1. −3π2 ms−2
2. 5π2 ms−2
3. −5π2 ms−2
4. 3π2 ms−2
A body describes simple harmonic motion with an amplitude of \(5~\text{cm}\) and a period of \(0.2~\text{s}\). What is the velocity of the body when the displacement is \(3~\text{cm}\)?
1. \(0.4\pi ~\text{m/s}\)
2. \(0\)
3. \(0.5\pi ~\text{m/s}\)
4. \(0.3\pi ~\text{m/s}\)
A mass attached to a spring is free to oscillate, with angular velocity \(\omega\), in a horizontal plane without friction or damping. It is pulled to a distance
1. \(\sqrt{\left(2x_0^2+\frac{v_0^2}{\omega^2}\right)} \)
2. \(\sqrt{\left(x_0^2+\frac{v_0^2}{\omega^2}\right)} \)
3. \(\sqrt{\left(x_0^2+\frac{v_0^2}{2\omega^2}\right)} \)
4. \(\sqrt{\left( x_0^2+\frac{v_0^2}{\pi\omega^2}\right)} \)
Identify the correct definition:
| 1. | If after every certain interval of time, a particle repeats its motion, then the motion is called periodic motion. |
| 2. | To and fro motion of a particle is called oscillatory motion. |
| 3. | Oscillatory motion described in terms of single sine and cosine functions is called simple harmonic motion. |
| 4. | All of the above |
The displacement of a particle executing S.H.M. is given by x = 0.01sin100(t + 0.05). The time period is:
(1) 0.01 s
(2) 0.02 s
(3) 0.1 s
(4) 0.2 s
A boy is swinging in a swing. If he stands, the time period will:
(1) First decrease, then increase
(2) Decrease
(3) Increase
(4) Remain same
The time period of a simple pendulum in a freely falling lift will be:
(1) Finite
(2) Infinite
(3) Zero
(4) All of these
If the effective length of a simple pendulum is equal to the radius of the earth (R), the time period will be:
(1)
(2)
(3)
(4)






