To maintain a rotor at a uniform angular speed of \(200~\text{rad/s},\) an engine needs to transmit a torque of \(180~\text{N-m}.\) What is the power required by the engine?
1.  \(33~\text{kW}\)
2.  \(36~\text{kW}\)
3.  \(28~\text{kW}\)
4.  \(76~\text{kW}\)

A meter stick is balanced on a knife edge at its center. When two coins, each of the mass \(5\) gm are put one on top of the other at the \(12.0\) cm mark, the stick is found to be balanced at \(45.0\) cm. What is the mass of the meter stick?
1. \(66~\text{gm}\) 
2. \(56~\text{gm}\) 
3. \(76~\text{gm}\) 
4. \(79~\text{gm}\) 

A hoop of radius \(2\) m weighs \(100\) kg. It rolls along a horizontal floor so that its center of mass has a speed of \(20\) cm/s. How much work has to be done to stop it?
1. \(10\) J
2. \(9\) J
3. \(4\) J
4. \(6\) J

The oxygen molecule has a mass of \(5.30\times 10^{-26}~\text{kg}\) and a moment of inertia of \(1.94\times 10^{-46}~\text{kg m}^2\) about an axis through its center perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is \(500~\text{m/s}\) and that its kinetic energy of rotation is two-thirds of its kinetic energy of translation. The average angular velocity of the molecule is:
1. \(5.7\times 10^{11}~\text{rad/s}\)
2. \(5.7\times 10^{12}~\text{rad/s}\)
3. \(6.7\times 10^{11}~\text{rad/s}\)
4. \(6.7\times 10^{12}~\text{rad/s}\)

A solid cylinder rolls up an inclined plane of the angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s. How far will the cylinder go up the plane?

1. 4.9 m
2. 1.3 m
3. 4.7 m
4. 3.8 m

A man stands on a rotating platform, with his arms stretched horizontally holding a \(5~\text{kg} \) weight in each hand. The angular speed of the platform is \(30\) revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from \(90~\text{cm}\) to \(20~\text{cm}.\) The moment of inertia of the man together with the platform may be taken to be constant and equal to \( 7.6~\text{kg}~\text{m}^2.\) What is his new angular speed?
1. \(60~\text{rev/min}\)
2. \(57.0~\text{rev/min}\)
3. \(58.8~\text{rev/min}\)
4. \(60.1~\text{rev/min}\)

A bullet of mass \(10\) g and speed \(500\) m/s is fired into a door and gets embedded exactly at the center of the door. The door is \(1.0\) m wide and weighs \(12\) kg. It is hinged at one end and rotates about a vertical axis practically without friction. The angular speed of the door just after the bullet embeds into it is:
1. \(0.122\) rad/s
2. \(0.625\) rad/s
3. \(0.231\) rad/s
4. \(0.191\) rad/s

A disc rotating about its axis with angular speed ${\omega }_0$ is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. The linear velocities of the points A, B, and C on the disc (as shown in the figure) respectively are:
     
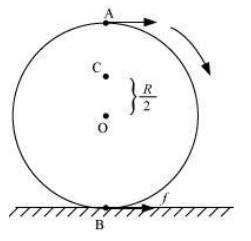
1. \(\omega_0 R, \omega_0 R, \frac{\omega_0 R}{2}\)
2. \(\frac{\omega_0 R}{2}, \omega_0 R, \omega_0 R\)
3. \(\omega_0 \mathrm{R}, \frac{\omega_0 \mathrm{R}}{2}, \omega_0 \mathrm{R}\)
4. \(\omega_0 R, \omega_0 R, 0\)

A cylinder of mass \(10\) kg and radius of \(15\) cm is rolling perfectly on a plane of inclination \(30^\circ.\) The coefficient of static friction \(\mu_s=0.25.\) How much is the force of friction acting on the cylinder?
1. \(16.3\) N
2. \(15.5\) N
3. \(19.1\) N
4. \(20.0\) N

Three point masses m₁, m₂ and m₃ are placed at the corners of a thin massless rectangular sheet (1.2 m x 1.0 m) as shown. Centre of mass will be located at the point

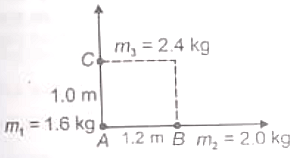
(1) (0.8, 0.6) m

(2) (0.6, 0.8) m

(3) (0.4, 0.4) m

(4) (0.5, 0.6) m