A particle is projected at a time \(t=0\) with a speed \(v_{0}\)${\mathrm{}}_{}$ and at an angle with the horizontal in a uniform gravitational field. Then which of the following graphs represents power delivered by the gravitational force against time \((t)?\)

1.		2.
3.		4.

The potential energy \(\mathrm{U}\) of a system is given by $\mathrm{U}=$ $\mathrm{A}$ $-$ ${\mathrm{Bx}}^2$ (where \(\mathrm{x}\) is the position of its particle and \(\mathrm{A},\) \(\mathrm{B}\) are constants). The magnitude of the force acting on the particle is:
1. constant

2. proportional to \(\mathrm{x}\)

3. proportional to ${\mathrm{x}}^2$

4. proportional to $\left(\frac{1}{\mathrm{x}}\right)$

A person-1 stands on an elevator moving with an initial velocity of 'v' & upward acceleration 'a'. Another person-2 of the same mass m as person-1 is standing on the same elevator. The work done by the lift on the person-1 as observed by person-2 in time 't' is:

1.  $\mathrm{m}\left(\mathrm{g}\right)$ $+$ $\mathrm{a}\left(\mathrm{vt}\right)$ $+$ $\frac{1}{2}{\mathrm{at}}^2$

2.  $-\mathrm{mg}\left(\mathrm{vt}\right)$ $+$ $\frac{1}{2}{\mathrm{at}}^2$

3.  0

4.  $\mathrm{ma}\left(\mathrm{vt}\right)$ $+$ $\frac{1}{2}{\mathrm{at}}^2$

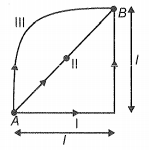
If a body of mass 2 kg is moved in the conservative field from point A to B in three different paths, then work done will be

(1)  ${\mathrm{W}}_{\mathrm{I}} < {\mathrm{W}}_{\mathrm{II}} < {\mathrm{W}}_{\mathrm{III}}$

(2)  ${\mathrm{W}}_{\mathrm{I}} > {\mathrm{W}}_{\mathrm{II}} > {\mathrm{W}}_{\mathrm{III}}$

(3)  ${\mathrm{W}}_{\mathrm{I}} = {\mathrm{W}}_{\mathrm{II}} = {\mathrm{W}}_{\mathrm{III}}$

(4)  ${\mathrm{W}}_{\mathrm{I}} > {\mathrm{W}}_{\mathrm{II}} = {\mathrm{W}}_{\mathrm{III}}$

A particle is moving along the x-axis under a conservative force and its potential energy U varies with x co-ordinate as shown in the figure. Then force is positive at:

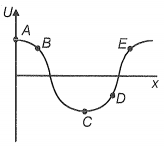
(1)  A

(2)  C, D 

(3)  B

(4)  D, E

A block of mass \(m\) is connected to a spring of force constant \(K.\) Initially, the block is at rest and the spring is relaxed. A constant force \(F\) is applied horizontally towards the right. The maximum speed of the block will be:

                         
1. \(\dfrac{F}{\sqrt{2mK}}\)

2. \(\dfrac{\sqrt{2}F}{\sqrt{mK}}\)

3. \(\dfrac{F}{\sqrt{mK}}\)

4. \(\dfrac{2F}{\sqrt{2mK}}\)

Two blocks A and B of mass m and 4m at rest are displaced through identical paths due to identical net forces, then

1.  Their speeds are in the ratio, $\frac{{\mathrm{v}}_{\mathrm{A}}}{{\mathrm{v}}_{\mathrm{B}}} = \frac{1}{1}$

2.  Work done on the blocks is in the ratio, $\frac{W_{\mathrm{A}}}{W_{\mathrm{B}}} = \frac{1}{1}$

3.  Their kinetic energies are in the ratio, $\frac{K_{\mathrm{A}}}{K_{\mathrm{B}}} = \frac{1}{4}$

4.  All of these

For the path wxyz in a conservative field, the amount of work done in carrying a body from w to x and from x to y and from y to z are 2 J. 4 J and 6 J respectively. The work done in carrying the body from w to z will be

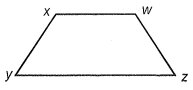
(1)  12 J

(2)  2 J

(3)  4 J

(4)  6