If a body starts its motion along the smooth track from P as shown in the figure, then its velocity at the instant of leaving R is

                              

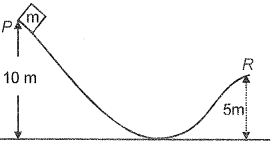
(1)  5 m/s 

(2)  15 m/s

(3)  10 m/s

(4)  20 m/s

The principle of conservation of energy and conservation of mechanical energy applicable respectively for

(1)  Conservative and non-conservative forces

(2)  Conservative and conservative force

(3)  Non-conservative and conservative forces

(4)  All forces and conservative forces

A ball of mass \(2\) kg is at rest on a horizontal smooth surface. Another ball of the same mass hit the first ball at an angle of \(60^{\circ}\) with the horizontal. At the time of the collision, the velocity of the second ball is \(20\) m/s. If the collision is perfectly inelastic and after the collision, both the balls stick together, then the speed of the combined balls is:

1. Zero

2. \(2.5\) m/s

3. \(10\) m/s

4. \(5\) m/s

A particle of mass m is moving in a vertical circle of radius r. If the velocity of the particle at the uppermost point is $\sqrt{2gr}$, then its velocity at the lowermost point

(1)  $\sqrt{7\mathrm{gr}}$

(2)  $\sqrt{6gr}$

(3)  $\sqrt{5gr}$

(4)  2$\sqrt{gr}$

A bullet is fired from a gun. Assuming that the gun recoils freely, the kinetic energy of the bullet is

(1)  less than the kinetic energy of the gun.

(2)  equal to the kinetic energy of the gun.

(3)  more than the kinetic energy of the gun.

(4)  equal to or less than the kinetic energy of the gun.

A person applies a force \(\vec F\) on a box inside a moving train. If \(S_1\) is the displacement of box with respect to train and \(S_2\) is the displacement of train with respect to ground, then the work done by the person in the frame of the earth will be:
1. \(\vec F \cdot \vec{S_1}\)
2. \(\vec F \cdot \vec{S_2}\)
3. \(\vec F \cdot (\vec{S_1}+ \vec{S_2})\)
4. \(\vec F \cdot (\vec{S_1}- \vec{S_2})\)

A block having mass m is hanging by a string of length l. A variable horizontal force is applied on the block, which displaces the block slowly till the string makes an angle $\mathrm{\theta }$ with the vertical. Find the work done by the force.

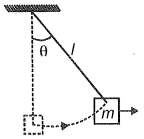
(1)  mgl

(2)  mgl(1 - cos$\mathrm{\theta }$)

(3)  mglcos$\mathrm{\theta }$

(4)  mgl(1 + cos$\mathrm{\theta }$)

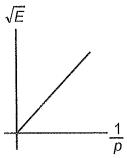
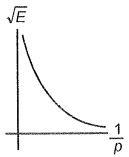
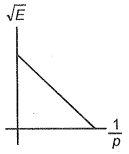
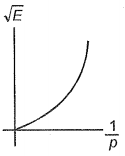
A particle is moving with kinetic energy E and momentum p. Which of the following graphs is possible between $\sqrt{E}$ and $\frac{1}{p}$?

1.  

2.  

3.  

4.  

Two vehicles are moving with the same kinetic energy. If the ratio of their masses is 1 : 3 then find the ratio of their stopping distances when both vehicles stop with the same retardation.

(1)  1: 1

(2)  3: 1

(3)  9: 1

(4)  1: 9

Two blocks having equal masses stick together after the collision. If their combined velocity after the collision is equal to the arithmetic mean velocity of them before the collision, then the coefficient of restitution is:

(1)  Zero

(2)  0.5

(3)  0.8

(4)  1