A block slides down an inclined plane of inclination \(30^{\circ}\) with a constant velocity. It then projected up with an initial speed of \(6~\text{m/s}\), the distance moved by it on the inclined before coming to rest is:
1. \(1.5~\text{m}\)
2. \(1.8~\text{m}\)
3. \(2.0~\text{m}\)
4. \(2.4~\text{m}\)

The potential energy of a particle of mass 0.5 kg moving along x axis is given by

U = 2x (x - 3). The speed of the particle is maximum at

(1)  x = 1 m

(2)  x = 1.5 m

(3)  X = 2 m

(4)  x = 3 m

Work energy theorem is valid in

(1)  Only inertial frame of reference

(2)  The only non-inertial frame of reference

(3)  Both inertial and non-inertial frame of reference

(4)  Does not depend on any frame of reference

A block of mass m is projected with speed v along the rough surface of an inclined plane of height h. If block comes to rest at the top of the surface, then work done by friction force is

1.  $-\frac{1}{2}{\mathrm{mv}}^2$

2.  $\mathrm{m}\left[\mathrm{gh} - \frac{1}{2}{\mathrm{v}}^2\right]$

3.  -mgh

4.  $\mathrm{m}\left[\mathrm{gh} + \frac{1}{2}{\mathrm{v}}^2\right]$

If a body starts its motion along the smooth track from P as shown in the figure, then its velocity at the instant of leaving R is

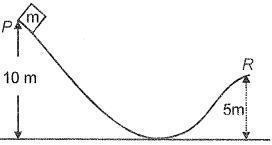
(1)  5 m/s 

(2)  15 m/s

(3)  10 m/s

(4)  20 m/s

The principle of conservation of energy and conservation of mechanical energy applicable respectively for

(1)  Conservative and non-conservative forces

(2)  Conservative and conservative force

(3)  Non-conservative and conservative forces

(4)  All forces and conservative forces

A particle of mass m is moving in a vertical circle of radius r. If the velocity of the particle at the uppermost point is $\sqrt{2gr}$, then its velocity at the lowermost point

(1)  $\sqrt{7\mathrm{gr}}$

(2)  $\sqrt{6gr}$

(3)  $\sqrt{5gr}$

(4)  2$\sqrt{gr}$

A person applies a force \(\vec F\) on a box inside a moving train. If \(S_1\) is the displacement of box with respect to train and \(S_2\) is the displacement of train with respect to ground, then the work done by the person in the frame of the earth will be:
1. \(\vec F \cdot \vec{S_1}\)
2. \(\vec F \cdot \vec{S_2}\)
3. \(\vec F \cdot (\vec{S_1}+ \vec{S_2})\)
4. \(\vec F \cdot (\vec{S_1}- \vec{S_2})\)

A block having mass m is hanging by a string of length l. A variable horizontal force is applied on the block, which displaces the block slowly till the string makes an angle $\mathrm{\theta }$ with the vertical. Find the work done by the force.

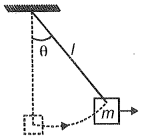
(1)  mgl

(2)  mgl(1 - cos$\mathrm{\theta }$)

(3)  mglcos$\mathrm{\theta }$

(4)  mgl(1 + cos$\mathrm{\theta }$)