The r.m.s. voltage of the waveform shown is:

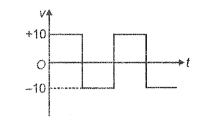
1. 10 V

2. 6.37 V

3. 7 V

4. 10.5 v

Voltage and current in an A.C. circuit is given by $V=20\sin \left(314t\right) V and l=10\sin \left(314t+\frac{\pi }{3}\right) A.$

Wattful current in the circuit is-

$1. 10 A$
$2. 5 A$
$3. \frac{5}{\sqrt{2}}A$
$4. \frac{10}{\sqrt{2}}A$

A time-varying current is given by $l=5\sin \left(\omega t+\begin{array}{c}\pi \\ 6\end{array}\right)$ Its r.m.s. value is (symbols have usual meanings)

$1. 5\sqrt{5} A$
$2. 10 A$
$3. \frac{5}{\sqrt{2}} A$
$4. \frac{15}{\sqrt{2}}A$

For the circuit shown in figure below, the ammeter $A_2$ reads 1.6 A and ammeter $A_3$ read 0.4 A If ${\omega }_0$ is angular frequency and $f$ is frequency of ac, then

$1. {\omega }_0=\frac{4}{\sqrt{LC}}$
$2. f=\frac{2\pi }{\sqrt{LC}}$
$3. The ammeter A_1 reads 1.2 A$
$4. The ammeter A_1 reads 2 A$

Given that the current \(i_1=3A \sin \omega t\) and the current \(i_2=4A \cos \omega t,\) what will be the expression for the current \(i_3\)?

                  
1. \(5 A \sin \left(\omega t+53^{\circ}\right) \)
2. \(5 A \sin \left(\omega t+37^{\circ}\right) \)
3. \(5 A \sin \left(\omega t+45^{\circ}\right) \)
4. \( 5 A \sin \left(\omega t+30^{\circ}\right)\)

In a box \(Z\) of unknown elements (\(L\) or \(R\) or any other combination), an ac voltage \(E = E_0 \sin(\omega t + \phi)\) $$is applied and the current in the circuit is found to be \(I = I_0 \sin\left(\omega t + \phi +\frac{\pi}{4}\right)\). The unknown elements in the box could be:
             

The phase difference between emf and current through the choke coil maybe

1. 0$°$

2. 85$°$

3. 45$°$

4. 30$°$