A particle is projected at an angle $\theta$ with horizontal with an initial speed u. When it makes an angle $\alpha$ with horizontal, its speed is:

1. $\mathrm{ucos\theta }$

2. $\mathrm{ucos\theta }\times \mathrm{ucos\alpha }$

3. $\frac{\mathrm{usin\theta }}{\mathrm{sin\alpha }}$

4. $\frac{\mathrm{ucos\theta }}{\mathrm{cos\alpha }}$

 

A particle is moving with velocity \(\overrightarrow{v} = k \left(y \hat{i} + x \hat{j}\right)\) where \(k\) is a constant. The general equation for the path will be:

A body is thrown vertically so as to reach its maximum height in \(t\) second. The total time from the time of projection to reach a point at half of its maximum height while returning (in second) is:
1. \(\sqrt{2} t\)
2. \(\left(1 + \frac{1}{\sqrt{2}}\right) t\)
3. \(\frac{3 t}{2}\)
4. \(\frac{t}{\sqrt{2}}\)

A projectile is given an initial velocity of $\hat{i}+2\hat{j}$. The cartesian equation of its path is (g = 10 ${\mathrm{ms}}^{-2}$) 

1. $\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

2. $\mathrm{y}=\mathrm{x}-5{\mathrm{x}}^2$

3. $4\mathrm{y}=2\mathrm{x}-5{\mathrm{x}}^2$

4. $\mathrm{y}=2\mathrm{x}-25{\mathrm{x}}^2$

Time taken by the projectile to reach from A to B is t. Then the distance AB is equal to :

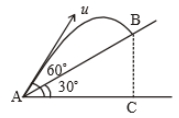
1. $\frac{ut}{\sqrt{3}}$

2. $\frac{\sqrt{3}ut}{2}$

3. $\sqrt{3}ut$

4. 2ut

Three particles are moving with constant velocities \(v_1 ,v_2\) and \(v\) respectively as given in the figure. After some time, if all the three particles are in the same line, then the relation among \(v_1 ,v_2\) and \(v\) is:
                            
1. \(v =v_1+v_2\)
2. \(v= \sqrt{v_{1} v_{2}}\)
3. \(v = \frac{v_{1} v_{2}}{v_{1} + v_{2}}\)
4. \(v=\frac{\sqrt{2} v_{1} v_{2}}{v_{1} + v_{2}}\)

A body is thrown horizontally with a velocity $\sqrt{2gh}$ from the top of a tower of height h. It strikes the level ground through the foot of the tower at a distance x from the tower. The value of x is:

(1) h

(2) $\frac{h}{2}$

(3) 2h

(4) $\frac{2h}{3}$

A particle starts from the origin at t=0 and moves in the x-y plane with a constant acceleration 'a' in the y direction. Its equation of motion is $y=b{x}^2$. The x component of its velocity (at t=0) will be:

1. variable

2. $\sqrt{\frac{2a}{b}}$

3. $\frac{a}{2b}$

4. $\sqrt{\frac{a}{2b}}$

A boat is sent across a river in perpendicular direction with a velocity of 8 km/hr. If the resultant velocity of boat is 10 km/hr, then velocity of the river is : 

(1) 10 km/hr

(2) 8 km/hr

(3) 6 km/hr

(4) 4 km/hr

A boat moves with a speed of \(5\) km/h relative to water in a river flowing with a speed of \(3\) km/h. Width of the river is \(1\) km. The minimum time taken for a round trip will be:
1. \(5\) min
2. \(60\) min
3. \(20\) min
4. \(30\) min