An incompressible liquid travels as shown in the figure. The speed of the fluid in the lower branch will :

1. 1 m/s
2. 1.5 m/s
3. 2.25 m/s
4. 3 m/s

The surface tension of a soap solution is \(2 \times 10^{-2}\) N/m. If a soap bubble with a radius of \(4\) cm is blown, the amount of work done is:
1. \(4\pi \times 10^{-6}~\text{J}\)
2. \(2.56\pi \times 10^{-4}~\text{J}\)
3. \(16\pi \times 10^{-5}~\text{J}\)
4. \(16\pi \times 10^{-6}~\text{J}\)
A small tiny water droplet is falling towards earth at a uniform speed of 1 cm/s. When 27 such identical droplets combine together to form a bigger drop, then with what uniform velocity will this bigger drop fall?
| 1. | 27 cm/s
|
2. | 9 cm/s
|
| 3. | 3 cm/s
|
4. | 81 cm/s |
The velocity of water in a river is:
| 1. | same everywhere. |
| 2. | more in the middle and less near its banks. |
| 3. | less in the middle and more at banks. |
| 4. | increases from one bank to other. |
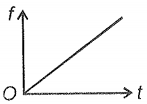
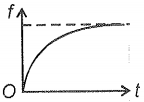
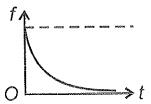
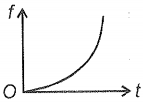
A steel ball is dropped on the water surface from zero height. The variation of the viscous force with time on the ball can be represented as
1. 
2. 
3. 
4. 
A body with an air cavity loses one-third of weight when immersed in water. If the relative density of the material of the body is 6, then the ratio of the volume of the cavity to the volume of the body is:
1.
2.
3.
4.
Which of the following graphs correctly shows the variation in kinetic energy (KE) of a metal sphere falling freely in a lake? Assume sufficient depth of the lake to impart terminal velocity to the sphere (d: depth)
1. 
3. 
If an incompressible liquid is flowing through a horizontal pipe having branches of area \({A},\) \(0.4{A},\) and \(0.5{A}\) as shown in the figure, then the value of \({v}\) is:

1. \(3.2~\text{m/s}\)
2. \(6.4~\text{m/s}\)
3. \(1.6~\text{m/s}\)
4. \(0.8~\text{m/s}\)
The continuity equation for fluid flow is based on the principle of the
(1) Conservation of mass
(2) Conservation of energy
(3) Conservation of momentum
(4) Conservation of angular momentum
Blood flows in an artery of radius R in a Laminar manner under pressure p with a flow rate Q. If the radius gets halved and the pressure quadruples, the new rate of flow will be
1. 4Q
2.
3. Q
4.








