Absolute refractive indices of glass and water are 3/2 and 4/3. The ratio of velocity of light in glass and water will be

1.  4:3

2.  8:7

3.  8:9

4.  3:4

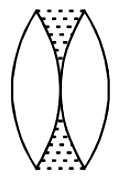
A thin equiconvex lens of power \(P\) is cut into three parts \(A,B,\) and \(C\) as shown in the figure. If \(P_1,P_2\) and \(P_3\) are powers of the three parts respectively, then:
            

Focal lengths of objective and eyepiece of a compound microscope are 2 cm and 6.25 cm respectively. An object AB is placed at a distance of 2.5 cm from the objective which forms the image B'A' as shown in the figure. Maximum magnifying power in this case is :

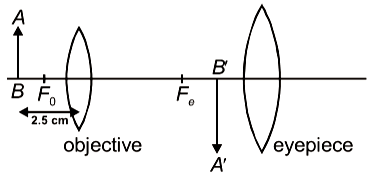
1.  10

2.  20

3.  5

4.  25

Two identical equiconvex thin lenses each of focal lengths 20 cm, made of material of refractive index 1.5 are placed coaxially in contact as shown. Now, the space between them is filled with a liquid of refractive index 1.5. The equivalent power of this arrangement will be:

1.  + 5D

2.  Zero

3.  + 2.5D

4.  + 0.5D

In the situation shown, the incident monochromatic ray retraces its path after its incidence on the silvered surface. The speed of light inside the prism will be

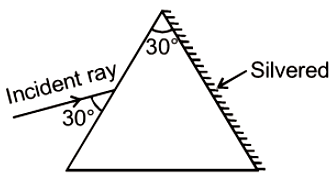
1.  $3 \mathrm{x} {10}^8 {\mathrm{ms}}^{-1}$

2.  $2 \mathrm{x} {10}^8 {\mathrm{ms}}^{-1}$

3.  $1.41 \mathrm{x} {10}^8 {\mathrm{ms}}^{-1}$

4.  $1.73 \mathrm{x} {10}^8 {\mathrm{ms}}^{-1}$

The sun (diameter D) subtends an angle $\mathrm{\theta }$ radian at the pole of a concave mirror of focal length f. The diameter of the image of the sun formed by the mirror is:

1.  $\mathrm{f\theta }$

2.  $2\mathrm{f\theta }$

3.  $\frac{2\mathrm{f\theta }}{\mathrm{D}}$

4.  $\mathrm{D\theta }$

The focal length of the plano-convex lens is 20 cm. If its plane surface is silvered, then

1.  it behaves as a concave mirror of focal length 10 cm

2.  it behaves as a convex mirror of  focal length of 10 cm

3.  it behaves as a concave mirror of focal length 20 cm

4.  none of these

A ray of light falls on a transparent sphere as shown in the figure. If the final ray emerges from the sphere parallel to the horizontal diameter, then calculate the refractive index of the sphere. Consider that the sphere is kept in the air.

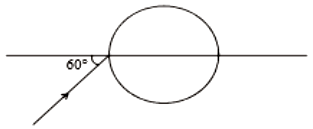
1.  $\sqrt{2}$ 

2.  $\sqrt{3}$

3.  $\sqrt{3/2}$

4.  $\sqrt{4/3}$

A point source of light \(B\) is placed at a distance \(L\) in front of the centre of a mirror of width \(d\) hung vertically on a wall. A man \((A)\) walks in front of the mirror along a line parallel to the mirror at a distance \(2L\) from it as shown. The greatest distance over which he can see the image of the light source in the mirror is:
                         
1. \(\frac{d}{2}\)
2. \(d\)
3. \(2d\)
4. \(3d\)

Two plane mirrors, A and B are aligned parallel to each other, as shown in the figure. A light ray is incident at an angle of $30°$ at a point just inside one end of A. The plane of incidence coincides with the plane of the figure. The maximum number of times the ray undergoes reflections (excluding the first one) before it emerges out is :

(a) 28                                     (b) 30

(c) 32                                      (d) 34