A planet whose density is double of earth and radius is half of the earth, will produce gravitational field on its surface:
(\(g=\) acceleration due to gravity at the surface of earth)
1.
\(g\)
2.
\(2g\)
3.
\(\dfrac{g}{2}\)
4.
\(3g\)
(\(g=\) acceleration due to gravity at the surface of earth)
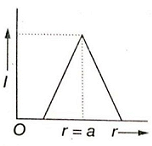
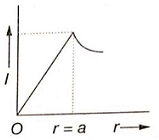
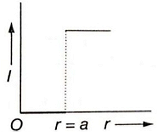
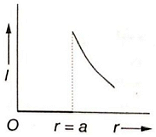
Which of the following graphs represents correctly the variation of intensity of gravitational field l with the distance r from the centre of a spherical shell of mass M and radius a?
1. 
2. 
3. 
4. 
A uniform spherical shell gradually shrinks maintaining its shape. The gravitational potential at the centre:
1. increases
2. decreases
3. remains constant
4. oscillates
A mass falls from a height \(h\) and its time of fall \(t\) is recorded in terms of time period \(T\) of a simple pendulum. On the surface of the earth, it is found that \(t=2T\). The entire setup is taken on the surface of another planet whose mass is half of that of the Earth and whose radius is the same. The same experiment is repeated and corresponding times are noted as \(t'\) and \(T'\). Then we can say:
1. \(t' = \sqrt{2}T\)
2. \(t'>2T'\)
3. \(t'<2T'\)
4. \(t' = 2T'\)
| 1. | \(6\sqrt{2}~\text{hr}\) | 2. | \(12\sqrt{2}~\text{hr}\) |
| 3. | \(\frac{24}{2.5}~\text{hr}\) | 4. | \(\frac{12}{2.5}~\text{hr}\) |
Assuming that the gravitational potential energy of an object at infinity is zero, the change in potential energy (final - initial) of an object of mass \(m\) when taken to a height \(h\) from the surface of the earth (of radius \(R\) and mass \(M\)), is given by:
| 1. | \(-\frac{GMm}{R+h}\) | 2. | \(\frac{GMmh}{R(R+h)}\) |
| 3. | \(mgh\) | 4. | \(\frac{GMm}{R+h}\) |
A particle of mass M is at distance 'a' from the surface of a thin spherical shell of mass M and radius a. If are the potentials at the centre and the surface of the shell respectively, then
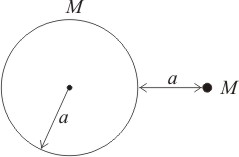
1.
2.
3.
4. Can't say
The distance between the centres of moon and earth is D. The mass of earth is 81 times the mass of the moon. At what distance from the centre of the earth the gravitational force will be zero ?
1. 2.
3. 4.
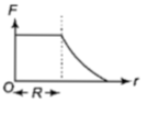
Which one of the following plots represent
the variation of gravitational field on a
particle at distance r, due to a thin
spherical shell of radius R? (r is measured
from the centre of the spherical shell).
1.
3. 
A body weighs \(200\) N on the surface of the earth. How much will it weigh halfway down the centre of the earth?
| 1. | \(100\) N | 2. | \(150\) N |
| 3. | \(200\) N | 4. | \(250\) N |






