13.7.3 Nuclear fusion – energy generation in stars

When two light nuclei fuse to form a larger nucleus, energy is released, since the larger nucleus is more tightly bound, as seen from the binding energy curve in Fig.13.1. Some examples of such energy liberating nuclear fusion reactions are :

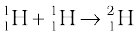+ e+ + ν + 0.42 MeV         [13.29(a)]

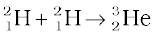+ n + 3.27 MeV           [13.29(b)]

+ 4.03 MeV        [13.29(c)]

In the first reaction, two protons combine to form a deuteron and a positron with a release of 0.42 MeV energy. In reaction [13.29(b)], two deuterons combine to form the light isotope of helium. In reaction (13.29c), two deuterons combine to form a triton and a proton. For fusion to take place, the two nuclei must come close enough so that attractive short-range nuclear force is able to affect them. However, since they are both positively charged particles, they experience coulomb repulsion. They, therefore, must have enough energy to overcome this coulomb barrier. The height of the barrier depends on the charges and radii of the two interacting nuclei. It can be shown, for example, that the barrier height for two protons is ~ 400 keV, and is higher for nuclei with higher charges. We can estimate the temperature at which two protons in a proton gas would (averagely) have enough energy to overcome the coulomb barrier:

(3/2)k T = K = 400 keV, which gives T ~ 3 × 109 K.

When fusion is achieved by raising the temperature of the system so that particles have enough kinetic energy to overcome the coulomb repulsive behaviour, it is called thermonuclear fusion.

Thermonuclear fusion is the source of energy output in the interior of stars. The interior of the sun has a temperature of 1.5×107 K, which is considerably less than the estimated temperature required for fusion of particles of average energy. Clearly, fusion in the sun involves protons whose energies are much above the average energy.

 The fusion reaction in the sun is a multi-step process in which the hydrogen is burned into helium. Thus, the fuel in the sun is the hydrogen in its core. The proton-proton (p, p) cycle by which this occurs is represented by the following sets of reactions:

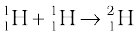+ e+ + ν + 0.42 MeV      (i)

e+ + e– → γ + γ + 1.02 MeV          (ii)

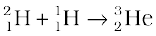+ γ + 5.49 MeV          (iii)

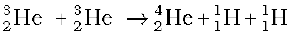+ 12.86 MeV      (iv)           (13.30)

For the fourth reaction to occur, the first three reactions must occur twice, in which case two light helium nuclei unite to form ordinary helium nucleus. If we consider the combination 2(i) + 2(ii) + 2(iii) +(iv), the net effect is

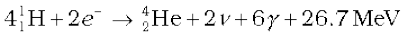
or 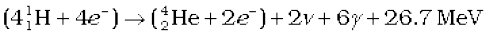(13.31)

Thus, four hydrogen atoms combine to form an 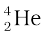atom with a release of 26.7 MeV of energy.

Helium is not the only element that can be synthesized in the interior of a star. As the hydrogen in the core gets depleted and becomes helium, the core starts to cool. The star begins to collapse under its own gravity which increases the temperature of the core. If this temperature increases to about 108 K, fusion takes place again, this time of helium nuclei into carbon. This kind of process can generate through fusion higher and higher mass number elements. But elements more massive than those near the peak of the binding energy curve in Fig. 13.1 cannot be so produced.

The age of the sun is about 5×109 y and it is estimated that there is enough hydrogen in the sun to keep it going for another 5 billion years. After that, the hydrogen burning will stop and the sun will begin to cool and will start to collapse under gravity, which will raise the core temperature. The outer envelope of the sun will expand, turning it into the so called red giant.